Markov number

The first levels of the Markov number tree

A Markov number or Markoff number is a positive integer x, y or z that is part of a solution to the Markov Diophantine equation

$x^2 + y^2 + z^2 = 3xyz,\,$

studied by Andrey Markoff (1879, 1880).

The first few Markov numbers are

1, 2, 5, 13, 29, 34, 89, 169, 194, 233, 433, 610, 985, 1325, ... (sequence A002559 in OEIS)

appearing as coordinates of the Markov triples

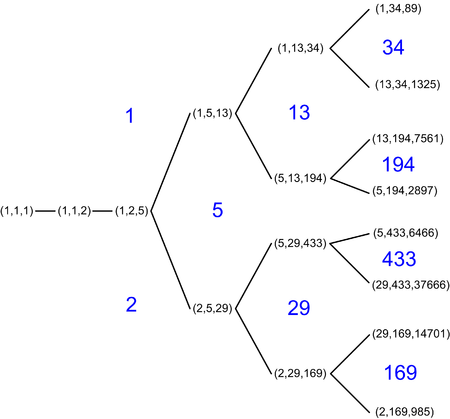
(1, 1, 1), (1, 1, 2), (1, 2, 5), (1, 5, 13), (2, 5, 29), (1, 13, 34), (1, 34, 89), (2, 29, 169), (5, 13, 194), (1, 89, 233), (5, 29, 433), (89, 233, 610), etc.

There are infinitely many Markov numbers and Markov triples.

Markov tree

There are two simple ways to obtain a new Markov triple from an old one (x, y, z). First, one may permute the 3 numbers x,y,z, so in particular one can normalize the triples so that x ≤ y ≤ z. Second, if (x, y, z) is a Markov triple then so is (x, y, 3xy − z). Applying this operation twice returns the same triple one started with. Joining each normalized Markov triple to the 1, 2, or 3 normalized triples one can obtain from this gives a graph starting from (1,1,1) as in the diagram. This graph is connected; in other words every Markov triple can be connected to (1,1,1) by a sequence of these operations. If we start, as an example, with (1, 5, 13) we get its three neighbors (5, 13, 194), (1, 13, 34) and (1, 2, 5) in the Markov tree if x is set to 1, 5 and 13, respectively. For instance, starting with (1, 1, 2) and trading y and z before each iteration of the transform lists Markov triples with Fibonacci numbers. Starting with that same triplet and trading x and z before each iteration gives the triples with Pell numbers.

All the Markov numbers on the regions adjacent to 2's region are odd-indexed Pell numbers (or numbers n such that 2n² − 1 is a square,  A001653), and all the Markov numbers on the regions adjacent to 1's region are odd-indexed Fibonacci numbers ( A001519). Thus, there are infinitely many Markov triples of the form

$(1, F_{2n - 1}, F_{2n + 1}),\,$

where F_x is the xth Fibonacci number. Likewise, there are infinitely many Markov triples of the form

$(2, P_{2n - 1}, P_{2n + 1}),\,$

where P_x is the xth Pell number.^[1]

Other properties

Aside from the two smallest triples, every Markov triple (a,b,c) consists of three distinct integers.

The unicity conjecture states that for a given Markov number c, there is exactly one normalized solution having c as its largest element.

Odd Markov numbers are 1 more than multiples of 4, while even Markov numbers are 2 more than multiples of 32.^[2]

In his 1982 paper, Don Zagier conjectured that the nth Markov number is asymptotically given by

$m_n = \tfrac13 e^{C\sqrt{n}+o(1)} \quad\text{with } C = 2.3523418721 \ldots.$

Moreover he pointed out that x² + y² + z² = 3xyz + 4 / 9, an extremely good approximation of the original Diophantine equation, is equivalent to f(x) + f(y) = f(z) with f(t) = arcosh(3t/2).^[3]

The nth Lagrange number can be calculated from the nth Markov number with the formula

$L_n = \sqrt{9 - {4 \over {m_n}^2}}.\,$

Markov's theorem

Markoff (1879, 1880) showed that if

$f(x,y) = ax^2+bxy+cy^2 \,$

is an indefinite binary quadratic form with real coefficients, then there are integers x, y for which it takes a nonzero value of absolute value at most

$\frac{D}{3}=\frac{b^2-4ac}{3}$

unless f is a constant times a form

$px^2+(3p-2a)xy+(b-3a)y^2 \,$

where (p, q, r) is a Markov triple and

$0<a<p/2,aq\equiv\pm r\bmod p, bp-a^2=1 \,$

Matrices

If X and Y are in SL₂(C) then

Tr(X)Tr(Y)Tr(XY) + Tr(XYX ^{− 1}Y ^{− 1}) + 2 = Tr(X)² + Tr(Y)² + Tr(XY)²

so that if Tr(XYX⁻¹Y⁻¹)=−2 then

Tr(X)Tr(Y)Tr(XY) = Tr(X)² + Tr(Y)² + Tr(XY)²

In particular if X and Y also have integer entries then Tr(X)/3, Tr(Y)/3, and Tr(XY)/3 are a Markov triple. If XYZ = 1 then Tr(XY) = Tr(Z), so more symmetrically if X, Y, and Z are in SL₂(Z) with XYZ = 1 and the commutator of two of them has trace −2, then their traces/3 are a Markov triple.

See also

• Markov spectrum

Notes

1. ^  A030452 lists Markov numbers that appear in solutions where one of the other two terms is 5.
2. ^ Zhang, Ying (2007). "Congruence and Uniqueness of Certain Markov Numbers". Acta Arithmetica 128 (3): 295–301. doi:10.4064/aa128-3-7. MR2313995. http://journals.impan.gov.pl/aa/Inf/128-3-7.html. 
3. ^ Zagier, Don B. (1982). "On the Number of Markoff Numbers Below a Given Bound". Mathematics of Computation 160 (160): 709–723. doi:10.2307/2007348. JSTOR 2007348. MR0669663. 

References

• Thomas Cusick, Mari Flahive: The Markoff and Lagrange spectra, Math. Surveys and Monographs 30, AMS, Providence 1989
• Richard K. Guy (2004). Unsolved Problems in Number Theory. Springer-Verlag. pp. 263–265. ISBN 0-387-20860-7. 
• Malyshev, A.V. (2001), "Markov spectrum problem", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/m/m062540.htm 
• Markoff, A. (1879). "Sur les formes quadratiques binaires indéfinies". Mathematische Annalen (Springer Berlin / Heidelberg) 15 (3–4): 381–406. doi:10.1007/BF02086269. ISSN 0025-5831 
• Markoff, A. (1880). "Sur les formes quadratiques binaires indéfinies". Mathematische Annalen (Springer Berlin / Heidelberg) 17 (3): 379–399. doi:10.1007/BF01446234. ISSN 0025-5831