Polyiamond

A polyiamond (also polyamond or simply iamond) is a polyform whose base form is an equilateral triangle. The word polyiamond is a back-formation from diamond, because this word is often used to describe the shape of a pair of equilateral triangles placed base to base, and the initial "di-" looked like a Greek prefix meaning "two-".

Counting polyiamonds

The basic combinatorial question is how many different polyiamonds exist with a given number of cells. Like polyominoes, polyiamonds may be free or one-sided. Free polyiamonds are invariant under reflection as well as translation and rotation. One-sided polyiamonds distinguish reflections.

The number of free n-iamonds for n = 1, 2, 3, … is (sequence A000577 in OEIS):

1, 1, 1, 3, 4, 12, 24, 66, 160, …

The number of free polyiamonds with holes is given by  A070764; the number of free polyiamonds without holes is given by  A070765; the number of fixed polyiamonds is given by  A001420; the number of one-sided polyiamonds is given by  A006534.

Name	Number of forms	Forms
Moniamond	1
Diamond	1
Triamond	1
Tetriamond	3
Pentiamond	4
Hexiamond	12

Symmetries

Possible symmetries are mirror symmetry, 2-, 3-, and 6-fold rotational symmetry, and each combined with mirror symmetry.

2-fold rotational symmetry with and without mirror symmetry requires at least 2 and 4 triangles, respectively. 6-fold rotational symmetry with and without mirror symmetry requires at least 6 and 18 triangles, respectively. Asymmetry requires at least 5 triangles. 3-fold rotational symmetry without mirror symmetry requires at least 7 triangles.

In the case of only mirror symmetry we can distinguish having the symmetry axis aligned with the grid or rotated 30° (requires at least 4 and 3 triangles, respectively); ditto for 3-fold rotational symmetry, combined with mirror symmetry (requires at least 18 and 1 triangles, respectively).

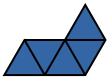
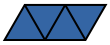
Asymmetric	Mirror, 0°	Mirror, 30°	Rotational, 2-Fold	Mirror, 2-Fold
Rotational, 3-Fold	Mirror, 0°, 3-fold	Mirror, 30°, 3-fold	Rotational, 6-Fold	Mirror, 6-Fold

Generalizations

Like polyominoes, but unlike polyhexes, polyiamonds have three-dimensional counterparts, formed by aggregating tetrahedra. However, polytetrahedra do not tile 3-space in the way polyiamonds can tile 2-space.

Tessellations

Every polyiamond of order 6 or less tiles the plane. All but one of the heptiamonds tile the plane.^[1]

Correspondence with Polyhexes

Pentiamond with corresponding pentahex superimposed.

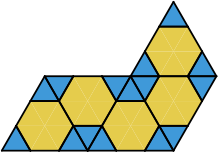
Every polyiamond corresponds to a polyhex, as illustrated at right. Conversely, every polyhex is also a polyiamond, because each hexagonal cell of a polyhex is the union of six adjacent equilateral triangles.

See also

• Tessellation
• Percolation theory

External links

• Weisstein, Eric W., "Polyiamond" from MathWorld.
• VERHEXT — a 1960s puzzle game by Heinz Haber based on hexiamonds

References

1. ^ http://www.mathpuzzle.com/Tessel.htm