n-flake

An n-flake, polyflake, or Sierpinski n-gon,^[1] is a fractal constructed starting from an n-gon. This n-gon is replaced by a flake of smaller n-gons, such that the scaled polygons are placed at the vertices, and sometimes in the center. This process is repeated recursively to result in the fractal. Typically, there is also the restriction that the n-gons must touch yet not overlap.

In two dimensions

The most common variety of n-flake is two-dimensional (in terms of its topological dimension) and is formed of polygons. The four most common special cases are formed with triangles, squares, pentagons, and hexagons, but it can be extended to any polygon.^[2] Its boundary is the von Koch curve of varying types – depending on the n-gon – and infinitely many Koch curves are contained within. The fractals occupy zero area yet have an infinite perimeter.

The formula of the scale factor r for any n-flake is:^[3]

$r = \frac{1}{2\left(1 + \displaystyle \sum_{k=1}^{\lfloor n/4 \rfloor} {\cos \frac{2 \pi k}{n}}\right)}$

where cosine is evaluated in radians and n is the number of sides of the n-gon. The Hausdorff dimension of a n-flake is $\textstyle \frac{\log m}{\log r}$, where m is the number of polygons in each individual flake and r is the scale factor.

Sierpinski triangle

The Sierpinski triangle is an n-flake formed by successive flakes of three triangles. Each flake is formed by placing triangles scaled by 1/2 in each corner of the triangle they replace. Its Hausdorff dimension is equal to $\textstyle{\frac {\log(3)} {\log(2)}}$ ≈ 1.585. The $\textstyle{\frac {\log(3)} {\log(2)}}$ is obtained because each iteration has 3 triangles that are scaled by 1/2.

• 

  The sixth iteration of the Sierpinski triangle.

• 

  The Sierpinski triangle created by the chaos game.

Vicsek fractal

If a sierpinski 4-gon were constructed from the given definition, the scale factor would be 1/2 and the fractal would simply be a square. A more interesting alternative, the Vicsek fractal, rarely called a quadraflake, is formed by successive flakes of five squares scaled by 1/3. Each flake is formed either by placing a scaled square in each corner and one in the center or one on each side of the square and one in the center. Its Hausdorff dimension is equal to $\textstyle{\frac {\log(5)} {\log(3)}}$ ≈ 1.4650. The $\textstyle{\frac {\log(5)} {\log(3)}}$ is obtained because each iteration has 5 squares that are scaled by 1/3. The boundary of the Vicsek Fractal is a Type 1 quadratic Koch curve.

• 

  The fifth iteration of the Vicsek fractal.

Pentaflake

A pentaflake, or sierpinski pentagon, is formed by successive flakes of six regular pentagons.^[4] Each flake is formed by placing a pentagon in each corner and one in the center. Its Hausdorff dimension is equal to $\textstyle{\frac {\log(6)} {\log(1+\varphi)}}$ ≈ 1.8617, where $\textstyle{\varphi = \frac{1+\sqrt 5}{2}}$ (golden ratio). The $\textstyle{\frac {\log(6)} {\log(1+\varphi)}}$ is obtained because each iteration has 6 pentagons that are scaled by $\textstyle{\frac {1} {1+\varphi}}$. The boundary of a pentaflake is the Koch curve of 72 degrees.

There is also a variation of the pentaflake that has no central pentagon. Its Hausdorff dimension equals $\textstyle{\frac {\log(5)} {\log(1+\varphi)}}$ ≈ 1.6723. This variation still contains infinitely many Koch curves, but they are somewhat more visible.

• 

  The third iteration of the pentaflake.

• 

  The fourth iteration of the pentaflake.

• 

  The fifth iteration of the pentaflake.

• 

  Variation of the pentaflake without central pentagon; third iteration.

Hexaflake

A hexaflake, or sierpinski hexagon, is formed by successive flakes of seven regular hexagons. Each flake is formed by placing a scaled hexagon in each corner and one in the center. Its Hausdorff dimension is equal to $\textstyle{\frac {\log(7)} {\log(3)}}$ ≈ 1.7712. The $\textstyle{\frac {\log(7)} {\log(3)}}$ is obtained because each iteration has 7 hexagons that are scaled by 1/3. The boundary of a hexaflake is the standard Koch curve of 60 degrees and infinitely many Koch snowflakes are contained within. Also, the projection of the cantor cube onto the plane orthogonal to its main diagonal is a hexaflake.

Like the pentaflake, there is also a variation of the hexaflake that has no central hexagon. Its Hausdorff dimension equals $\textstyle{\frac {\log(6)} {\log(3)}}$ ≈ 1.6309. This variation still contains infinitely many Koch curves of 60 degrees.

• 

  The hexaflake.

• 

  The first six iterations of the hexaflake.

• 

  Third iteration of the hexaflake variant that lacks a central hexagon.

• 

  Orthogonal projection of a cantor cube showing a hexaflake.

Polyflake

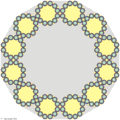
n-flakes of higher polygons also exist, though they are less common and don't usually have a central polygon. Some examples are shown below; the 8-flake, 10-flake, and 12-flake. While it may not be obvious, these higher polyflakes still contain infinitely many Koch curves, but the angle of the Koch curves decreases as n increases. Their Hausdorff dimensions are slightly more difficult to calculate than lower n-flakes because their scale factor is less obvious. However, the Hausdorff dimension is always less than two but no less than one. An interesting n-flake is the ∞-flake, because as the value of n increases, an n-flake's Hausdorff dimension approaches 1,^[5] and when n is infinite, the dimension is 1 and the fractal is a circle.^[5]

• 

  The third iteration of the octoflake or 8-flake.

• 

  The third iteration of the decaflake or 10-flake.

• 

  The third iteration of the dodecaflake or 12-flake.

In three dimensions

n-flakes can generalized to higher dimensions, in particular to a topological dimension of three.^[6] Instead of polygons, regular polyhedra are iteratively replaced. However, while there are an infinite number of regular polygons, there are only five regular, convex polyhedra. Because of this, three-dimensional n-flakes are also called platonic solid fractals.^[7] In three dimensions, the fractals' volume is zero.

Sierpinski tetrahedron

A Sierpinski tetrahedron is formed by successive flakes of four regular tetrahedrons. Each flake is formed by placing a tetrahedron scaled by 1/2 in each corner. Its Hausdorff dimension is equal to $\textstyle{\frac {\log(4)} {\log(2)}}$, which is exactly equal to 2. On every face there is a Sierpinski triangle and infinitely many are contained within.

• 

  The third iteration of the Sierpinksi tetrahedron.

Hexahedron flake

A hexahedron, or cube, flake defined in the same way as the Sierpinski tetrahedron is simply a cube^[8] and is not interesting as a fractal. However, there are two pleasing alternatives. One is the Menger Sponge, where every cube is replaced by a three dimensional ring of cubes. Its Hausdorff dimension is $\textstyle{\frac {\log(20)} {\log(3)}}$ ≈ 2.7268.

Another hexahedron flake can be produced in a manner similar to the Vicsek fractal extended to three dimensions. Every cube is divided into 27 smaller cubes and the center cross is retained, which is the opposite of the Menger sponge where the cross is removed. However, it is not the Menger Sponge complement. Its Hausdorff dimension is $\textstyle{\frac {\log(7)} {\log(3)}}$ ≈ 1.7712, because a cross of 7 cubes, each scaled by 1/3, replaces each cube.

• 

  The fourth iteration of the Menger Sponge.

• 

  Third iteration of the 3D Vicsek fractal.

Octahedron flake

An octahedron flake, or sierpinski octahedron, is formed by successive flakes of six regular octahedrons. Each flake is formed by placing a octahedron scaled by 1/2 in each corner. Its Hausdorff dimension is equal to $\textstyle{\frac {\log(6)} {\log(2)}}$ ≈ 2.5849. On every face there is a Sierpinski triangle and infinitely many are contained within.

• 

  The third iteration of the Octahedron flake.

Dodecahedron flake

A dodecahedron flake, or sierpinski dodecahedron, is formed by successive flakes of twenty regular dodecahedrons. Each flake is formed by placing a dodecahedron scaled by $\textstyle{\frac {1} {2+\varphi}}$ in each corner. Its Hausdorff dimension is equal to $\textstyle{\frac {\log(20)} {\log(2+\varphi)}}$ ≈ 2.3296.

• 

  The second iteration of the dodecaedron fractal flake.

Icosahedron flake

An icosahedron flake, or sierpinski icosahedron, is formed by successive flakes of twelve regular icosahedrons. Each flake is formed by placing a icosahedron scaled by $\textstyle{\frac {1} {1+\varphi}}$ in each corner. Its Hausdorff dimension is equal to $\textstyle{\frac {\log(12)} {\log(1+\varphi)}}$ ≈ 2.5819.

• 

  The third iteration of the icosahedron fractal flake.

See also

• List of fractals by Hausdorff dimension

References

1. ^ Dennis, Kevin; Schlicker, Steven, Sierpinski n-Gons, p. 1, http://faculty.gvsu.edu/schlicks/SNGONS4.pdf 
2. ^ Dennis, Kevin; Schlicker, Steven, Sierpinski n-Gons, p. 2, http://faculty.gvsu.edu/schlicks/SNGONS4.pdf 
3. ^ Riddle, Larry. "Sierpinski n-gons". http://ecademy.agnesscott.edu/~lriddle/ifs/pentagon/sierngon.htm. Retrieved 9 May 2011. 
4. ^ Weisstein, Eric W., "Pentaflake" from MathWorld.
5. ^ ^{a b} Dennis, Kevin; Schlicker, Steven, Sierpinski n-Gons, p. 7, http://faculty.gvsu.edu/schlicks/SNGONS4.pdf 
6. ^ Kunnen, Aimee; Schlicker, Steven, Regular Sierpinski Polyhedra, http://faculty.gvsu.edu/schlicks/phdra.pdf 
7. ^ Paul Bourke (December 2005). "Platonic solid fractals and their complements". http://local.wasp.uwa.edu.au/~pbourke/fractals/platonic/. Retrieved 22 January 2011. 
8. ^ Kunnen, Aimee; Schlicker, Steven, Regular Sierpinski Polyhedra, p. 3, http://faculty.gvsu.edu/schlicks/phdra.pdf 

External links

• Quadraflakes, Pentaflakes, Hexaflakes and more – includes Mathematica code to generate these fractals