Mundell–Fleming model

The Mundell–Fleming model, also known as the IS-LM-BP model, is an economic model first set forth (independently) by Robert Mundell and Marcus Fleming.^[1][2] The model is an extension of the IS-LM model. Whereas the traditional IS-LM Model deals with economy under autarky (or a closed economy), the Mundell–Fleming model describes an open economy.

The Mundell-Fleming model portrays the short-run relationship between an economy's nominal exchange rate, interest rate, and output (in contrast to the closed-economy IS-LM model, which focuses only on the relationship between the interest rate and output). The Mundell–Fleming model has been used to argue that an economy cannot simultaneously maintain a fixed exchange rate, free capital movement, and an independent monetary policy. This principle is frequently called "the Unholy Trinity," the "Irreconcilable Trinity," the "inconsistent trinity" or the Mundell–Fleming "trilemma."

Basic set up

The Mundell-Fleming model is based on the following equations.

• $Y=C+I+G+NX \,$ (the IS curve)
  • where $Y \,$ is GDP, C is consumption, I is physical investment, G is government spending and NX is net exports.

• $\frac{M}{P}=L(i, Y)$ (The LM Curve)
  • where M is the nominal money supply, P is the price level, L is liquidity preference ( real money demand), and i is the nominal interest rate. A higher interest rate or a lower income (GDP) level leads to lower money demand.

• $BoP=CA+KA \,$ (The BoP Curve (Balance of Payments))
  • where BoP is the balance of payments surplus, $CA \,$ is the current account surplus, and KA is the capital account surplus.

IS components

• $C=C (Y-T(Y), i-E( \pi )) \,$
  • where C is consumption, Y is GDP, T is taxes, i is the nominal interest rate, and E(π) is the expected rate of inflation. Higher disposable income or a lower real interest rate (nominal interest rate minus expected inflation) leads to higher consumption spending.

• $I=I(i-E(\pi), Y_{-1}) \,$
  • where I is physical investment and Y _{− 1} is GDP in the previous period. Higher lagged income or a lower real interest rate leads to higher investment spending.

• G, government spending, is an exogenous variable.

• NX = NX(e,Y,Y * )
  • where NX is net exports, e is the nominal exchange rate (the price of domestic currency in terms of units of the foreign currency), Y is GDP, and Y * is the combined GDP of countries that are foreign trading partners. Higher domestic income (GDP) leads to more spending on imports and hence lower net exports; higher foreign income leads to higher spending by foreigners on the country's exports and thus higher net exports. A higher e (more expensive domestic currency in terms of foreign currency, and equivalently less expensive foreign currency in terms of domestic currency) leads to more purchasing of foreign goods due to the lesser cost of acquiring the foreign currency to pay for them, and also leads to less purchasing of the country's exports by foreigners since they find it more costly to acquire the country's currency with which to pay for them; for both reasons, higher e leads to lower net exports.

Balance of payments (BoP) components

• CA = NX
  • where CA is the current account and NX is net exports. That is, the current account is viewed as consisting solely of imports and exports.

• KA = z(i − i * ) + k
  • where i * is the foreign interest rate, k is the exogenous component of financial capital flows, z(.) is the interest-sensitive component of capital flows, and the derivative of the function z is the degree of capital mobility (the effect of differences between domestic and foreign interest rates upon capital flows KA). This derivative is positive if there is any capital mobility (since a higher relative domestic interest rate makes funds more prone to flow into the country), and it is infinitely positive if there is perfect capital mobility.

Variables determined by the model

After the subsequent equations are substituted into the first three equations above, one has a system of three equations in three unknowns, two of which are GDP and the domestic interest rate. Under flexible exchange rates, the exchange rate is the third endogenous variable while BoP is set equal to zero. In contrast, under fixed exchange rates e is exogenous and the balance of payments surplus is determined by the model.

Under both types of exchange rate regime, the nominal domestic money supply M is exogenous, but for different reasons. Under flexible exchange rates, the nominal money supply is completely under the control of the central bank. But under fixed exchange rates, the money supply in the short run (at a given point in time) is fixed based on past international money flows, while as the economy evolves over time these international flows cause future points in time to inherit higher or lower (but pre-determined) values of the money supply.

Mechanics of the model

The model's workings can be described in term of an IS-LM-BoP graph with the domestic interest rate plotted vertically and real GDP plotted horizontally. The IS curve is downward sloped and the LM curve is upward sloped, as in the closed economy IS-LM analysis; the BoP curve is upward sloped unless there is perfect capital mobility, in which case it is horizontal at the level of the world interest rate.

In this graph, under less than perfect capital mobility the positions of both the IS curve and the BoP curve depend on the exchange rate (as discussed below), since the IS-LM graph is actually a two-dimensional cross-section of a three- dimensional space involving all of the interest rate, income, and the exchange rate. However, under perfect capital mobility the BoP curve is simply horizontal at a level of the domestic interest rate equal to the level of the world interest rate.

Under a flexible exchange rate regime

In a system of flexible exchange rates, central banks allow the exchange rate to be determined by market forces alone.

Changes in the money supply

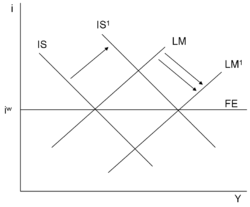
An increase in money supply shifts the LM curve to the right. This directly reduces the local interest rate relative to the global interest rate. This depreciates the exchange rate of local currency through capital outflow. (To the extent that funds are internationally mobile, they flow out to take advantage of the interest rate abroad, which has become relatively more attractive, and hence the currency depreciates.) The depreciation makes local goods cheaper compared to foreign goods, and this increases exports and decreases imports. Hence, net exports are increased. Increased net exports lead to the shifting of the IS curve (which is Y = C + I + G + NX) to the right, partially or entirely mitigating the initial decline in the domestic interest rate. At the same time, the BoP curve shifts rightward, since with a depreciated currency it takes a lower interest rate or higher income level to give a zero balance of payments surplus (which is what the curve describes). The combined effect of these three curves shifting is to increase the economy's income.

A decrease in the money supply causes the exact opposite process.

Changes in government spending

An increase in government expenditure shifts the IS curve to the right. The shift causes both the local interest rate and income (GDP) to rise. The increase in the local interest rate causes increased capital inflows, and the inflows make the local currency stronger compared to foreign currencies. On the other hand, the higher GDP increases spending on imports, tending to make the currency weaker. Assuming the BoP curve is not as steep as the LM curve (i.e., assuming that capital mobility is relatively strong), the former effect will dominate and the currency will become stronger. The stronger exchange rate also makes foreign goods cheaper compared to local goods. This encourages greater imports and discourages exports, so net exports become lower. As a result of this exchange rate change, the IS curve shifts back toward its original location. The stronger currency also shifts the BoP curve upward, as higher levels of the interest rate would now be consistent with a zero payments surplus in the presence of the stronger currency exchange rate. The LM curve is not at all affected in the short run. The net effect of all this is that, if there is perfect capital mobility, the level of income of the local economy is unchanged from originally, while it has gone up if capital is less than perfectly mobile.

A decrease in government expenditure reverses the process.

Changes in the global interest rate

An increase in the global interest rate shifts the BoP curve upward and causes capital flows out of the local economy. This depreciates the local currency and boosts net exports, shifting the IS curve to the right. Under less than perfect capital mobility, the depreciated exchange rate shifts the BoP curve somewhat back down. The net effect is an increase in income and the local interest rate.

Under perfect capital mobility, the BoP curve is always horizontal at the level of the world interest rate. When the latter goes up, the BoP curve shifts upward by the same amount, and stays there. The exchange rate changes enough to shift the IS curve to the location where it crosses the new BoP curve at its intersection with the unchanged LM curve; now the domestic interest rate equals the new level of the global interest rate.

A decrease in the global interest rate causes the reverse to occur.

Under a fixed exchange rate regime

In a system of fixed exchange rates, central banks announce an exchange rate (the parity rate) at which they are prepared to buy or sell any amount of domestic currency. Thus net payments flows into or out of the country need not equal zero; the exchange rate e is exogenously given, while the variable BoP is endogenous.

Under the fixed exchange rate system, the central bank operates in the foreign exchange market to maintain a specific exchange rate. If there is pressure to depreciate the domestic currency's exchange rate because the supply of domestic currency exceeds its demand in foreign exchange markets, the local authority buys domestic currency with foreign currency to decrease the domestic currency's supply in the foreign exchange market. This keeps the domestic currency's exchange rate at its targeted level. If there is pressure to appreciate the domestic currency's exchange rate because the currency's demand exceeds its supply in the foreign exchange market, the local authority buys foreign currency with domestic currency to increase the domestic currency's supply in the foreign exchange market. Again,this keeps the exchange rate at its targeted level.

Changes in the money supply

In the very short run the money supply is normally predetermined by the past history of international payments flows. If the central bank is maintaining an exchange rate that is consistent with a balance of payments surplus, over time money will flow into the country and the money supply will rise (and vice versa for a payments deficit). If the central bank were to conduct open market operations in the domestic bond market in order to offset these balance-of-payments-induced changes in the money supply — a process called sterilization, it would absorb newly arrived money by decreasing its holdings of domestic bonds (or the opposite if money were flowing out of the country). But under perfect capital mobility, any such sterilization would be met by further offsetting international flows.

Changes in government expenditure

An increase in government spending forces the monetary authority to supply the market with local currency to keep the exchange rate unchanged. Shown here is the case of perfect capital mobility, in which the BoP curve (or, as denoted here, the FE curve) is horizontal.

Increased government expenditure shifts the IS curve to the right. The shift results in an incipient rise in the interest rate, and hence upward pressure on the exchange rate (value of the domestic currency) as foreign funds start to flow in, attracted by the higher interest rate. However, the exchange rate is controlled by the local monetary authority in the framework of a fixed exchange rate system. To maintain the exchange rate and eliminate pressure on it, the monetary authority purchases foreign currencies with local currency until the pressure is gone. Such action, by increasing the domestic money supply, shifts the LM curve rightward in tandem with the IS shift. This action increases the local currency supply in the market and counters the upward pressure on the exchange rate. In the end, the exchange rate stays the same but the general income in the economy increases. In the IS-LM-BoP graph, the IS curve has been shifted exogenously by the fiscal authority, and the IS and BoP curves determine the final resting place of the system; the LM curve merely passively reacts.

The reverse process applies when government expenditure decreases.

Changes in the global interest rate

To maintain the fixed exchange rate, the central bank must accommodate the capital flows (in or out) which are caused by a change of the global interest rate, in order to offset pressure on the exchange rate.

If the global interest rate increases, shifting the BoP curve upward, capital flows out to take advantage of the opportunity. This puts pressure on the home currency to depreciate, so the central bank must buy the home currency — that is, sell some of its foreign currency reserves — to accommodate this outflow. The decrease in the money supply resulting from the outflow shifts the LM curve to the left until it intersect the IS and BoP curves at their intersection. Once again, the LM curve plays a passive role, and the outcomes are determined by the IS-BoP interaction.

Under perfect capital mobility, the new BoP curve will be horizontal at the new world interest rate, so the equilibrium domestic interest rate will equal the world interest rate.

If the global interest rate declines below the domestic rate, the opposite occurs. The BoP curve shifts down, foreign money flows in and the home currency is pressured to appreciate, so the central bank offsets the pressure by selling domestic currency (equivalently, buying foreign currency). The inflow of money causes the LM curve to shift to the right, and the domestic interest rate becomes lower (as low as the world interest rate if there is perfect capital mobility).

Differences from IS-LM

It is worth noting that some of the results from this model differ from those of the IS-LM model because of the open economy assumption. Results for a large open economy, on the other hand, can be consistent with those predicted by the IS-LM model. The reason is that a large open economy has the characteristics of both an autarky and a small open economy. In particular, it may not face perfect capital mobility, thus allowing internal policy measures to affect the domestic interest rate, and it may be able to sterilize balance-of-payments-induced changes in the money supply (as discussed above).

In the IS-LM model, the domestic interest rate is a key component in keeping both the money market and the goods market in equilibrium. Under the Mundell–Fleming framework of a small economy facing perfect capital mobility, the domestic interest rate is fixed and equilibrium in both markets can only be maintained by adjustments of the nominal exchange rate or the money supply (by international funds flows).

Example

The Mundell–Fleming model applied to a small open economy facing perfect capital mobility, in which the domestic interest rate is exogenously determined by the world interest rate, shows stark differences from the closed economy model.

Consider an exogenous increase in government expenditure. Under the IS-LM model, the IS curve shifts upward, with the LM curve intact, causing the interest rate and output to rise. But for a small open economy with perfect capital mobility and a flexible exchange rate, the domestic interest rate is predetermined by the horizontal BoP curve, and so by the LM equation given previously there is exactly one level of output that can make the money market be in equilibrium at that interest rate. Any exogenous changes affecting the IS curve (such as government spending changes) will be exactly offset by resulting exchange rate changes, and the IS curve will end up in its original position, still intersecting the LM and BoP curves at their intersection point.

The Mundell–Fleming model under a fixed exchange rate regime also has completely different implications from those of the closed economy IS-LM model. In the closed economy model, if the central bank expands the money supply the LM curve shifts out, and as a result income goes up and the domestic interest rate goes down. But in the Mundell-Fleming open economy model with perfect capital mobility, monetary policy becomes ineffective. An expansionary monetary policy resulting in an incipient outward shift of the LM curve would make capital flow out of the economy. The central bank under a fixed exchange rate system would have to instantaneously intervene by selling foreign money in exchange for domestic money to maintain the exchange rate. The accommodated monetary outflows exactly offset the intended rise in the domestic money supply, completely offsetting the tendency of the LM curve to shift to the right, and the interest rate remains equal to the world rate of interest.

See also

• Optimum currency area

References

1. ^ Mundell, Robert A. (1963). "Capital mobility and stabilization policy under fixed and flexible exchange rates". Canadian Journal of Economic and Political Science 29 (4): 475–485. doi:10.2307/139336.  Reprinted in Mundell, Robert A. (1968). International Economics. New York: Macmillan. 
2. ^ Fleming, J. Marcus (1962). "Domestic financial policies under fixed and floating exchange rates". IMF Staff Papers 9: 369–379.  Reprinted in Cooper, Richard N., ed (1969). International Finance. New York: Penguin Books. 

Further reading

• Young, Warren; Darity, William, Jr. (2004), "IS-LM-BP: An Inquest", History of Political Economy 36 (Suppl 1): 127–164, doi:10.1215/00182702-36-Suppl_1-127, http://www.econ.ucdavis.edu/faculty/kdhoover/pdf/Hope/Young.pdf  (Tells the difference between the IS-LM-BP model and the Mundell–Fleming model.)
• Carlin, Wendy; Soskice, David W. (1990), Macroeconomics and the Wage Bargain, New York: Oxford University Press, ISBN 0198772459 
• Mankiw, N. Gregory (2007), Macroeconomics (6th ed.), New York: Worth, ISBN 9780716762133 
• Blanchard, Olivier (2006), Macroeconomics (4th ed.), Upper Saddle River, NJ: Prentice Hall, ISBN 0131860267 
• DeGrauwe, Paul (2000), Economics of Monetary Union (4th ed.), New York: Oxford University Press, ISBN 0198776322