Multiple-prism dispersion theory

The first description of multiple-prism arrays, and multiple-prism dispersion, was given by Newton in his book Opticks.^[1] Prism pair expanders were introduced by Brewster in 1813.^[2] A modern mathematical description of the single-prism dispersion was given by Born and Wolf in 1959.^[3] The generalized multiple-prism dispersion theory was introduced by Duarte and Piper^[4][5] in 1982.

Generalized multiple-prism dispersion equations

A two-prism pulse compressor as deployed in some femtosecond laser configurations.

The generalized mathematical description of multiple-prism dispersion, as a function of the angle of incidence, prism geometry, prism refractive index, and number of prisms, was introduced as a design tool for multiple-prism grating laser oscillators by Duarte and Piper,^[4][5] and is given by

$(\partial\phi_{2,m}/\partial\lambda) = H_{2,m} (\partial n_m/\partial\lambda) + (k_{1,m}k_{2,m})^{-1}\bigg(H_{1,m}(\partial n_m/\partial\lambda) + (\partial\phi_{2,(m-1)}/\partial\lambda)\bigg)$

$(\partial\phi_{2,m}/\partial\lambda) = H_{2,m} (\partial n_m/\partial\lambda) + (k_{1,m}k_{2,m})^{-1}\bigg(H_{1,m}(\partial n_m/\partial\lambda) - (\partial\phi_{2,(m-1)}/\partial\lambda)\bigg)$

This multiple-prism arrangement is used with a diffraction grating to provide tuning in a dye laser.

where

$\,k_{1,m}=cos\psi_{1,m}/cos\phi_{1,m}$

$\,k_{2,m}=cos\phi_{2,m}/cos\psi_{2,m}$

$\,H_{1,m}=(tan\phi_{1,m})/n_m$

$\,H_{2,m}=(tan\phi_{2,m})/n_m$

Here, ϕ_1,m is the angle of incidence, at the mth prism, and ψ_1,m its corresponding angle of refraction. Similarly, ϕ_2,m is the exit angle and ψ_2,m its corresponding angle of refraction. The two main equations give the first order dispersion for an array of m prisms at the exit surface of the mth prism. The plus sign in the second term in parenthesis refers to a positive dispersive configuration while the minus sign refers to a compensating configuration.^[4][5] The k factors are the corresponding beam expansions, and the H factors are additional geometrical quantities. It can also be seen that the dispersion of the mth prism depends on the dispersion of the previous prism (m - 1).

These equations can also be used to quantify the angular dispersion in prism arrays, as described in Isaac Newton's book Opticks, and as deployed in dispersive instrumentation such as multiple-prism spectrometers. A comprehensive review on practical multiple-prism beam expanders and multiple-prism angular dispersion theory is given by Duarte.^[6]

More recently the generalized multiple-prism dispersion theory has been extended to higher order phase derivatives using a Newtonian iterative approach.^[7] This extension of the theory enables the evaluation of the Nth higher derivative via an elegant mathematical framework. Applications include further refinements in the design of prism pulse compressors and nonlinear optics.

For a single right-angled prism (m = 1) with the beam exiting normal to the output face, that is ϕ_2,m equal to zero, the Duarte-Piper equation reduces to^[6]

$(\partial\phi_{2,1}/\partial\lambda) = tan\psi_{1,1} (\partial n_1/\partial\lambda)$

Applications

The first application of this theory was to evaluate the laser linewidth in multiple-prism grating laser oscillators.^[4] Adding the grating contribution to the dispersion renders an equation for the total intracavity angular dispersion.^[4] It is this total dispersion that plays an important role in the linewidth narrowing of pulsed tunable lasers through the equation

$\Delta\lambda \approx \Delta \theta \left({\partial\theta\over\partial\lambda}\right)^{-1}$

where the angular dispersion is the quantity in parenthesis (elevated to –1). Although originally classical in origin, in 1992 it was shown that this cavity linewidth equation can also be derived from from quantum principles.^[8]

In 1987 the multiple-prism angular dispersion theory was extended to provide explicit second order equations directly applicable to the design of prismatic pulse compressors.^[9] The generalized multiple-prism dispersion theory is applicable to:

• laser microscopy,^[10][11]
• narrow-linewidth tunable laser design,^[12]
• prismatic beam expanders^[4][5]
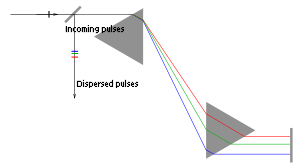
• prism compressors for femtosecond pulse lasers.^[13][14][15]

See also

• Beam expander
• Laser linewidth
• Multiple-prism grating laser oscillator

References

1. ^ I. Newton, Opticks (Royal Society, London, 1704).
2. ^ D. Brewster, A Treatise on New Philosophical Instruments for Various Purposes in the Arts and Sciences with Experiments on Light and Colours (Murray and Blackwood, Edinburgh, 1813).
3. ^ M. Born and E. Wolf, Principles of Optics, 7th Ed. (Cambridge University, Cambridge, 1999).
4. ^ ^{a b c d e f} F. J. Duarte and J. A. Piper, "Dispersion theory of multiple-prism beam expanders for pulsed dye lasers", Opt. Commun. 43, 303–307 (1982).
5. ^ ^{a b c d} F. J. Duarte and J. A. Piper, "Generalized prism dispersion theory", Am. J. Phys. 51, 1132–1134 (1982).
6. ^ ^{a b} F. J. Duarte, Tunable Laser Optics (Elsevier Academic, New York, 2003) Chapter 4.
7. ^ F. J. Duarte, Generalized multiple-prism dispersion theory for laser pulse compression: higher order phase derivatives, Appl. Phys. B 96, 809-814 (2009).
8. ^ F. J. Duarte, Cavity dispersion equation: a note on its origin, Appl. Opt. 31, 6979-6982 (1992).
9. ^ F. J. Duarte, "Generalized multiple-prism dispersion theory for pulse compression in ultrafast dye lasers", Opt. Quantum Electron. 19, 223–229 (1987)
10. ^ B. A. Nechay, U. Siegner, M. Achermann, H. Bielefeldt, and U. Keller, Femtosecond pump-probe near-field optical microscopy, Rev. Sci. Instrum. 70, 2758-2764 (1999).
11. ^ U. Siegner, M. Achermann, and U. Keller, Spatially resolved femtosecond spectroscopy beyond the diffraction limit, Meas. Sci. Technol. 12, 1847-1857 (2001).
12. ^ F. J. Duarte, Tunable Laser Optics (Elsevier Academic, New York, 2003) Chapter 7.
13. ^ L. Y. Pang, J. G. Fujimoto, and E. S. Kintzer, Ultrashort-pulse generation from high-power diode arrays by using intracavity optical nonlinearities, Opt. Lett. 17, 1599-1601 (1992).
14. ^ K. Osvay, A. P. Kovács, G. Kurdi, Z. Heiner, M. Divall, J. Klebniczki, and I. E. Ferincz, Measurement of non-compensated angular dispersion and the subsequent temporal lengthening of femtosecond pulses in a CPA laser, Opt. Commun. 248, 201-209 (2005).
15. ^ J. C. Diels and W. Rudolph, Ultrashort Laser Pulse Phenomena, 2nd Ed. (Elsevier Academic, New York, 2006).

External links

• References on multiple-prism dispersion theory
• Prism and Multiple-Prism Pulse Compression: Tutorial

This science article is a stub. You can help Wikipedia by expanding it.v · Categories: Science stubs Optics Nonlinear optics Prisms Wikimedia Foundation. 2010. Игры ⚽ Нужен реферат? Wikipedia:Multiple-place names Multiple-prism grating laser oscillator Look at other dictionaries: Multiple-prism grating laser oscillator — Multiple prism grating laser oscillators,[1] or MPG laser oscillators, use multiple prism beam expansion to illuminate a diffraction grating mounted either in Littrow configuration or grazing incidence configuration. Originally, these narrow… …   Wikipedia Prism (optics) — For other uses, see Prism (disambiguation). A plastic prism In optics, a prism is a transparent optical element with flat, polished surfaces that refract light. The exact angles between the surfaces depend on the application. The traditional… …   Wikipedia Prism compressor — A prism compressor is an optical device used to shorten the duration of a positively chirped ultrashort laser pulse by giving different wavelength components a different time delay. It typically consists of two prisms and a mirror. Figure 1 shows …   Wikipedia Dispersion (optics) — This article is about dispersion of waves in optics. For other forms of dispersion, see Dispersion (disambiguation). In a prism, material dispersion (a wavelength dependent refractive index) causes different colors to refract at different angles …   Wikipedia Dispersive prism — Photograph of a triangular prism, dispersing light …   Wikipedia Opticks — For other uses of Opticks , see Opticks (disambiguation). The first, 1704, edition of Opticks or a treatise of the reflections, refractions, inflections and colours of light …   Wikipedia Isaac Newton — Sir Isaac Newton …   Wikipedia F. J. Duarte — is a laser physicist based in Rochester, New York, USA. He is the author of several books on tunable lasers and introduced the generalized multiple prism dispersion theory.External links* [http://www.opticsjournal.com/fjduarte.htm] (online page) …   Wikipedia Dye laser — Close up of a table top dye laser based on Rhodamine 6G, emitting at 580 nm (yellow orange). The emitted laser beam is visible as faint yellow lines. The orange dye solution enters the laser from the left, and is pumped by a 514 nm (blue green)… …   Wikipedia Opticks — La première édition de 1704 La quatrième édition de 1730 …   Wikipédia en Français 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”