Rayleigh–Bénard convection

Bénard cells.

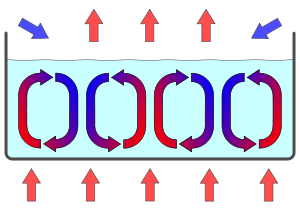
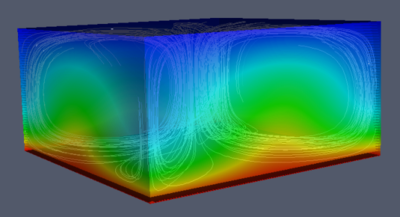
Rayleigh–Bénard convection is a type of natural convection, occurring in a plane of fluid heated from below, in which the fluid develops a regular pattern of convection cells known as Bénard cells. Rayleigh–Bénard convection is one of the most commonly studied convection phenomena because of its analytical and experimental accessibility.^[1] The convection patterns are the most carefully examined example of self-organizing nonlinear systems^[1].

Buoyancy, and hence gravity, is responsible for the appearance of convection cells. The initial movement is the upwelling of warmer liquid from the heated bottom layer.^[2] This upwelling spontaneously organizes into a regular pattern of cells.

Physical processes

The features of Rayleigh–Bénard convection can be obtained by a simple experiment first conducted by Henri Bénard, a French physicist, in 1900.

Development of convection

Convection cells in a gravity field

The experimental set-up uses a layer of liquid, e.g. water, between two parallel planes. The height of the layer is small compared to the horizontal dimension. At first, the temperature of the bottom plane is the same as the top plane. The liquid will then tend towards an equilibrium, where its temperature is the same as its surroundings. (Once there, the liquid is perfectly uniform: to an observer it would appear the same from any position. This equilibrium is also asymptotically stable: after a local, temporary perturbation of the outside temperature, it will go back to its uniform state, in line with the second law of thermodynamics).

Then, the temperature of the bottom plane is increased slightly yielding a flow of thermal energy conducted through the liquid. The system will begin to have a structure of thermal conductivity: the temperature, and the density and pressure with it, will vary linearly between the bottom and top plane. A uniform linear gradient of temperature will be established. (This system may be modelled by statistical mechanics).

Once conduction is established, the microscopic random movement spontaneously becomes ordered on a macroscopic level, forming Bénard convection cells, with a characteristic correlation length.

Convection features

Simulation of Rayleigh–Bénard convection in 3D.

The rotation of the cells is stable and will alternate from clock-wise to counter-clockwise horizontally; this is an example of spontaneous symmetry breaking. Bénard cells are metastable. This means that a small perturbation will not be able to change the rotation of the cells, but a larger one could affect the rotation; they exhibit a form of hysteresis.

Moreover, the deterministic law at the microscopic level produces a non-deterministic arrangement of the cells: if the experiment is repeated, a particular position in the experiment will be in a clockwise cell in some cases, and a counter-clockwise cell in others. Microscopic perturbations of the initial conditions are enough to produce a (non-deterministic) macroscopic effect. This inability to predict long-range conditions and sensitivity to initial-conditions are characteristics of chaotic or complex systems (i.e., the butterfly effect).

If the temperature of the bottom plane was to be further increased, the structure would become more complex in space and time; the turbulent flow would become chaotic.

Convective Bénard cells tend to approximate regular right hexagonal prisms, particularly in the absence of turbulence^[3][4][5], although certain experimental conditions can result in the formation of regular right square prisms^[6] or spirals^[7].

The Rayleigh–Bénard Instability

Since there is a density gradient between the top and the bottom plate, gravity acts trying to pull the cooler, denser liquid from the top to the bottom. This gravitational force is opposed by the viscous damping force in the fluid. The balance of these two forces is expressed by a non-dimensional parameter called the Rayleigh number. The Rayleigh Number is defined as:

$\mathrm{Ra}_{L} = \frac{g \beta} {\nu \alpha} (T_u - T_b) L^3$

where

• T_u is the Temperature of the top plate
• T_b is the Temperature of the bottom plate
• L is the height of the container.
• g is the acceleration due to gravity.
• ν is the kinematic viscosity.
• α is the Thermal diffusivity
• β is the Thermal expansion coefficient

As the Rayleigh number increases, the gravitational forces become more dominant. At a critical Rayleigh number of 1708, the instability sets in, and convection cells appear.

The critical Rayleigh number can be obtained analytically for a number of different boundary conditions by doing a perturbation analysis on the linearized equations in the stable state.^[8] The simplest case is that of two free boundaries, which Lord Rayleigh solved in 1916.^[9] and obtained R_c = ²⁷⁄₄ π⁴ ≈ 657.51.^[10] In the case of a rigid boundary at the bottom, and a free boundary at the top (which is the situation in an kettle without a lid), the critical Rayleigh number comes out as R_c = 1,100.65.^[11]

Effects of surface tension

Main article: Marangoni effect

In case of a free liquid surface in contact with air, buoyancy and surface tension effects will also play a role in how the convection patterns develop. Liquids flow from places of lower surface tension to places of higher surface tension. This is called the Marangoni effect. When applying heat from below, the temperature at the top layer will show temperature fluctuations. With increasing temperature, surface tension decreases. Thus a lateral flow of liquid at the surface will take place, from warmer areas to cooler areas. In order to preserve a horizontal (or nearly horizontal) liquid surface, cooler surface liquid will descend. This down-welling of cooler liquid contributes to the driving force of the convection cells. The specific case of temperature gradient-driven surface tension variations is known as thermo-capillary convection, or Bénard–Marangoni convection.

History and nomenclature

Rayleigh–Bénard convection, whose effects are due solely to a temperature gradient, was observed originally by Rayleigh; Bénard discovered thermo-capillary convection, which involves surface tension. Nonetheless in modern usage "Rayleigh–Bénard convection" refers to the effects due to temperature, whereas "Bénard–Marangoni convection" refers specifically to the effects of surface tension^[1].

Rayleigh–Bénard convection is also sometimes known as "Bénard–Rayleigh convection", "Bénard convection", or "Rayleigh convection".

References

1. ^ ^{a b c} Getling, A. V. (1998). Rayleigh–Bénard Convection: Structures and Dynamics. World Scientific. ISBN 978-9810226572. 
2. ^ "Rayleigh–Benard Convection". UC San Diego, Department of Physics. Archived from the original on 22 January 2009. http://replay.waybackmachine.org/20090222182327/http://physics.ucsd.edu/was-daedalus/convection/rb.html. 
3. ^ Rayleigh–Benard Convection Cells, with photos, from the Environmental Technology Laboratory at the National Oceanic and Atmospheric Administration in the United States Department of Commerce.
4. ^ http://www.edata-center.com/proceedings/1bb331655c289a0a,088ce8ea747789cd,59d115f133a4fd07.html
5. ^ http://cat.inist.fr/?aModele=afficheN&cpsidt=17287579
6. ^ http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=13973
7. ^ http://www.psc.edu/science/Gunton/gunton.html
8. ^ http://home.iitk.ac.in/~sghorai/NOTES/benard/benard.html
9. ^ http://www.informaworld.com/smpp/content~db=all~content=a910329374
10. ^ http://home.iitk.ac.in/~sghorai/NOTES/benard/node14.html
11. ^ http://home.iitk.ac.in/~sghorai/NOTES/benard/node16.html

External links

• A. Getling, O. Brausch: Cellular flow patterns
• K. Daniels, B. Plapp, W.Pesch, O. Brausch, E. Bodenschatz: Undulation Chaos in inclined Layer Convection