Dynamic rectangle

A dynamic rectangle is a right-angled, four-sided figure (a rectangle) with dynamic symmetry, which in this case, means that aspect ratio (height divided by width) is a distinguished value in dynamic symmetry, a proportioning system and natural design methodology described in Jay Hambidge's books. These dynamic rectangles begin with a square, which is extended (using a series of arcs and cross points) to form the desired figure, which can be the golden rectangle (1 : 1.618...), the 2:3 rectangle, the double square (1:2), or a root rectangle (1:√φ, 1:√2, 1:√3, 1:√5, etc.).^[1][2][3]

Root rectangles

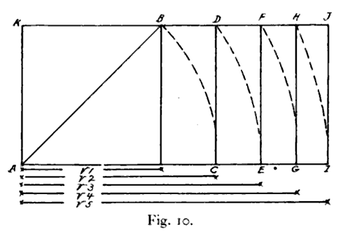Hambidge's 1920 illustration of the construction of root rectangles. The lengths of the horizontal sides of the original square and the four root rectangles derived from it, are respectively $\scriptstyle \sqrt{1}, \sqrt{2}, \sqrt{3}, \sqrt{4}, \sqrt{5}$.^[2]

A root rectangle is a rectangle in which the ratio of the longer side to the shorter is the square root of an integer, such as √2, √3, etc.^[2]

The root-2 rectangle (ACDK in Fig. 10) is constructed by extending two opposite sides of a square to the length of the square's diagonal. The root-3 rectangle is constructed by extending the two longer sides of a root-2 rectangle to the length of the root-2 rectangle's diagonal. Each successive root rectangle is produced by extending a root rectangle's longer sides to equal the length of that rectangle's diagonal.^[4]

Properties

• When a root-N rectangle is divided into N congruent rectangles by dividing the longer edge into N segments, the resulting figures keep the root-N proportion (as illustrated above).^[5]

• The root-3 rectangle is also called sixton,^[6] and its short and longer sides are proportionally equivalent to the side and diameter of a hexagon.^[7]

• Since 2 is the square root of 4, the root-4 rectangle has a proportion 1:2, which means that it is equivalent to two squares side-by-side.^[7]

• The root-5 rectangle is related to the golden ratio (φ). The longer side is equal to one plus two times 1/φ (0.618...).^[7]

Root-φ rectangle

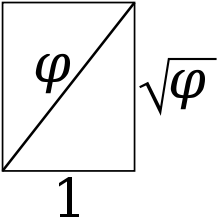A root-phi rectangle divides into a pair of Kepler triangles (right triangles with edge lengths in geometric progression).

The root-φ rectangle is a dynamic rectangle but not a root rectangle. Its diagonal equals φ times the length of the shorter side. If a root-φ rectangle is divided by a diagonal, the result is two congruent Kepler triangles.

Jay Hambidge

Jay Hambidge, as part of his theory of dynamic symmetry, includes the root rectangles in what he calls dynamic rectangles, which have irrational and geometric fractions as ratios, such as the golden ratio or square roots. Hambidge distinguishes these from rectangles with rational proportions, which he terms static rectangles.^[3] According to him, root-2, 3, 4 and 5 rectangles are often found in Gothic and Classical Greek and Roman art, objects and architecture, while rectangles with aspect ratios greater than root-5 are seldom found in human designs.^[4]

According to Matila Ghyka, Hambidge's dynamic rectangles

can produce the most varied and satisfactory harmonic (consonant, related by symmetry) subdivisions and combinations, and this by the very simple process [...] of drawing inside the chosen rectangle a diagonal and the perpendicular to it from one of the two remaining vertices (thus dividing the surface into a reciprocal rectangle and its gnomon) and the drawing any network of parallels and perpendiculars to sides and diagonals. This produces automatically surfaces correlated by the characteristic proportion of the initial rectangle and also avoids (automatically again) the mixing of antagonistic themes like √2 and √3 or √5. √5 and Φ on the contrary are not antagonistic but consonant, also with √Φ, Φ², et cetera.^[3]

Caskey's 1922 illustration of the property that a root-N rectangle divides into N reciprocal rectangles of the same proportions.^[8]

The 12 orthogons of Wersin

According to Wolfgang von Wersin's The Book of Rectangles, Spatial Law and Gestures of The Orthogons Described (1956), a set of 12 special orthogons (from the Gr. ορθος, orthos, "straight"^[9] and γονια, gonia, "angle"; "a right angled figure", which, as a consequence, is rectangular and tetragonal^[10]) has been used historically by artists, architects and calligraphers to guide the placement and interaction of elements in a design.^[3][11] These orthogons are:^[12]

• Square (1:1 or 1:√1)
• Diagon (1:√2)
• Hecton or sixton (1:√3)
• Doppelquadrat (1:2 or 1:√4)
• Hemiolion (2:3)
• Auron (the golden rectangle, 1:φ)
• Hemidiagon (1:½√5)
• Penton (1:√φ)
• Trion (1:⅔√3)
• Quadriagon
• Biauron (1:2φ)
• Bipenton

Wolfgang Von Wersin's book includes an extraordinary copy of text from the year 1558 (Renaissance), with diagrams of seven of the 12 orthogons and an invitation from the passage to pay careful attention as the "ancient" architects believed "nothing excels these proportions" as "a thing of the purest abstraction."^[13]

All 12 orthogons, when formed together, create an entire unit: a square that is developed into a double square.^[14]

Perhaps the most popular among the ortogons is the auron or golden rectangle, which is produced by projecting the diagonal that goes from the middle point of a side of a square to one of the opposite vertexes, until it is aligned with the middle point.

Four of these orthogons are harmonic rectangles: the diagon or root-2 rectangle is produced by projecting the diagonal of a square; the sixton, hecton or root-3 rectangle is produced by projecting the diagonal of a diagon; the double square or root-4 rectangle is produced by projecting the diagonal of an hecton; the root-5 rectangle is produced by projecting the diagonal of a double square (or by projecting 180° both diagonals that go from the middle point of a side of a square to the opposite vertexes).

Two of the most complicated of these figures are; the penton, with proportions 1:√φ is related to the section of the golden pyramid, the bipenton's longer side is equal to the shorter multiplied by two thirds of the square root of three, longer side of the biauron is √5 - 1 or 2τ times the shorter.

The quadriagon is related to the diagon in the sense that its longer side is produced by projecting the diagonal of a quarter of a square. The trion has the height of an equilateral triangle and the width of the side. The hemidiagon (1:½√5) longer side is half the one of the root-5 rectangle and is produced by projecting the diagonal of half a square until it is perpendicular with the origin.

Besides the square and the double square, the only other static rectangle included in the list is the hemiolion, which is produced by projecting 90° or 180° half the side of a square.

Constructing an orthogon

The dimensions of orthogons relate to each other and to the Orthogon as a whole. For this reason, use of Orthogons as a template or under-structure is of interest to artists, architects and designers.^[15]

Orthogons always begin with a square, any square. Once an individual Orthogon is constructed, additional related measurements are determined (small, medium, large). These measurements can then be used to guide the design (painting, architecture, pottery, furniture, calligraphy, auto, etc.).

Diagrams for all twelve orthogons are available.^[16]

Wersin's book has very detailed explanations for creating individual Orthogons.^[17] The measurements derived are then applied in a design. The artwork of Giorgio Morandi exemplifies how measurements of varying sizes (derived from an Orthogon) can create visual harmony.

Orthogons and design

Use of dimensions related to an orthogon as an under-structure system (or template for a design) ensures that the various parts will relate to the design as a whole. Marcus Vitruvius Pollio in Book Three of "De Architectura" (known currently as "The Ten Books of Architecture") explains:

"Therefore, since nature has designed the human body so that its members are duly proportioned to the frame as a whole, it appears that the ancients had good reason for their rule, that in perfect buildings the different members must be in exact symmetrical relations to the whole general scheme. Hence, while transmitting to us the proper arrangements for buildings of all kinds, they were particularly careful to do so in the case of temples of the gods, buildings in which merits and faults usually last forever."

Leonardo's drawing of the Vitruvian Man is an illustration of the concept of parts relating to the work as a whole.^[18]

References

1. ^ SKINNER, Stephen, Sacred Geometry Deciphering the Code, New York City: Sterling Publishing Company, 2006, pp. 53
2. ^ ^{a b c} Jay Hambidge (2003) [1920]. Dynamic Symmetry: The Greek Vase (Reprint of original Yale University Press edition ed.). Whitefish, MT: Kessinger Publishing. pp. 19–29. ISBN 0-7661-7679-7. http://books.google.com/books?id=Qq4gAAAAMAAJ&pg=PA19&dq=intitle:%22Dynamic+Symmetry%22+%22root+rectangles%22&ei=WTX2S5ffGYiIkgSNxoTJCQ&cd=1#v=onepage&q=intitle%3A%22Dynamic%20Symmetry%22%20%22root%20rectangles%22&f=false. 
3. ^ ^{a b c d} Matila Ghyka (1977). The Geometry of Art and Life. Courier Dover Publications. pp. 126–127. 
4. ^ ^{a b} Jay Hambidge. (1926, 1948, 1967)The Elements of Dynamic Symmetry. Courier Dover Publications. pp. 9–10.
5. ^ Andrew Haslam (2006). Book Design. Laurence King Publishing. pp. 48–49. ISBN 1856694739. http://books.google.com/books?id=_Ri63jEKPfgC&pg=PT27&dq=root-rectangle&as_brr=3&ei=N2wySKOPL4uKtAOk2NnvAg&sig=98V_Ww1L3EgAKmPofmkscnvxMsk. 
6. ^ Wim Muller (2001) Order and Meaning in Design. Lemma Publishers, p. 49.
7. ^ ^{a b c} Kimberly Elam (2001). Geometry of Design: Studies in Proportion and Composition. Princeton Architectural Press. pp. 34–41. ISBN 1568982496. http://books.google.com/books?id=1KI0JVuWYGkC&pg=PA41&dq=root-5+intitle:geometry+inauthor:elam&lr=&as_brr=0&as_pt=ALLTYPES&ei=KC-iSe--J4HqkwSx6OCNAg#PPA33,M1. 
8. ^ Lacey Davis Caskey (1922). Geometry of Greek Vases: Attic Vases in the Museum of Fine Arts Analysed According to the Principals of Proportion Discovered by Jay Hambidge. Museum of Fine Arts, Boston. http://books.google.com/books?id=6qNWAAAAMAAJ&pg=PA4&dq=inauthor:Lacey+inauthor:Davis+inauthor:Caskey+reciprocal&lr=&as_brr=0&ei=JOdFSNTEBpK2sgPmxqGxDQ. 
9. ^ "Ortho-", Oxford dictionary of current English, Oxford: Oxford University Press, 1998, pp. 627, 1071 p.
10. ^ CURTIS, Thomas, The London Encyclopaedia, 1829, pp. 356
11. ^ WERSIN, Wolfgang Von, Das Buch vom Rechteck Gesetz und Gestik des Raumlichen die Othogone-scheibe. Die Orthogone-scheibe (The Book of Rectangles, Spatial Law and Gestures of The Orthogons Described. The Orthogons Described), Ravensburg: Otto Maier Verlag Publishers, 1956
12. ^ WERSIN, pp. 83
13. ^ WERSIN, op. cit., pp. 36
14. ^ WERSIN, pp. 80
15. ^ http://www.constructingtheuniverse.com/Volume4.html
16. ^ "Constructie v/d harmonische Rechthoeken". http://alpha.uhasselt.be/~lucp1508/Harmonic/harmonic_rectangles.jpg. 
17. ^ WERSIN, pp. 82-85
18. ^ HEMENWAY, pp. 95

• Hemenway, Priya; Divine Proportion, Phi in Art, Nature and Science; 2005, Sterling Publishing Co., Inc, NY, NY.