Ramer–Douglas–Peucker algorithm

The Douglas–Peucker algorithm is an algorithm for reducing the number of points in a curve that is approximated by a series of points. The initial form of the algorithm was independently suggested in 1972 by Urs Ramer and 1973 by David Douglas and Thomas Peucker. (See the References for more details.) This algorithm is also known under the following names: the Ramer–Douglas–Peucker algorithm, the iterative end-point fit algorithm or the split-and-merge algorithm.

Idea

The purpose of the algorithm is, given a curve composed of line segments, to find a similar curve with fewer points. The algorithm defines 'dissimilar' based on the maximum distance between the original curve and the simplified curve. The simplified curve consists of a subset of the points that defined the original curve.

Algorithm

Smoothing a piecewise linear curve with the Douglas–Peucker algorithm.

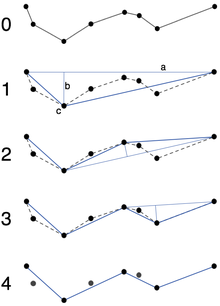
The starting curve is an ordered set of points or lines and the distance dimension ε > 0. The original (unsmoothed) curve is shown in 0 and the final output curve is shown in blue on row 4.

The algorithm recursively divides the line. Initially it is given all the points between the first and last point. It automatically marks the first and last point to be kept. It then finds the point that is furthest from the line segment with the first and last points as end points (this point is obviously furthest on the curve from the approximating line segment between the end points). If the point is closer than ε to the line segment then any points not currently marked to keep can be discarded without the smoothed curve being worse than ε.

If the point furthest from the line segment is greater than ε from the approximation then that point must be kept. The algorithm recursively calls itself with the first point and the worst point and then with the worst point and the last point (which includes marking the worst point being marked as kept).

When the recursion is completed a new output curve can be generated consisting of all (and only) those points that have been marked as kept.

Pseudocode

function DouglasPeucker(PointList[], epsilon)
 //Find the point with the maximum distance
 dmax = 0
 index = 0
 for i = 2 to (length(PointList) - 1)
  d = PerpendicularDistance(PointList[i], Line(PointList[1], PointList[end])) 
  if d > dmax
   index = i
   dmax = d
  end
 end
 
 //If max distance is greater than epsilon, recursively simplify
 if dmax >= epsilon
  //Recursive call
  recResults1[] = DouglasPeucker(PointList[1...index], epsilon)
  recResults2[] = DouglasPeucker(PointList[index...end], epsilon)
  
  // Build the result list
  ResultList[] = {recResults1[1...end-1] recResults2[1...end]}
 else
  ResultList[] = {PointList[1], PointList[end]}
 end
 
 //Return the result
 return ResultList[]
end

Application

The algorithm is used for the processing of vector graphics and cartographic generalization.

The algorithm is widely used in robotics^[1] to perform simplification and denoising of range data acquired by a rotating range scanner, in this field it is called the split-and-merge algorithm and is attributed to Duda and Hart.

Complexity

The expected complexity of this algorithm can be described by the linear recurrence $T(n) = 2T\left(\frac{n}{2}\right) + O(n)$, which has the well-known solution (via the Master Theorem) of $T(n) \in \Theta(n\log n)$. However, the worst case complexity is $O\left(n^2\right)$.

References

• Urs Ramer, "An iterative procedure for the polygonal approximation of plane curves", Computer Graphics and Image Processing, 1(3), 244–256 (1972) (DOI: 10.1016/S0146-664X(72)80017-0)

• David Douglas & Thomas Peucker, "Algorithms for the reduction of the number of points required to represent a digitized line or its caricature", The Canadian Cartographer 10(2), 112–122 (1973) (DOI: 10.3138/FM57-6770-U75U-7727)

• John Hershberger & Jack Snoeyink, "Speeding Up the Douglas–Peucker Line-Simplification Algorithm", Proc 5th Symp on Data Handling, 134–143 (1992). UBC Tech Report TR-92-07 available at http://www.cs.ubc.ca/cgi-bin/tr/1992/TR-92-07

• R.O. Duda and P.E. Hart, "Pattern classification and scene analysis", (1973), Wiley, New York (http://rii.ricoh.com/~stork/DHS.html)

Notes

1. ^ Nguyen and Martinelli and Siegwart (2005). "A Comparison of Line Extraction Algorithms using 2D Laser Rangefinder for Indoor Mobile Robotics". http://asl.epfl.ch/aslInternalWeb/ASL/publications/uploadedFiles/nguyen_2005_a_comparison_of.pdf. 

External links

• You can see the algorithm applied to a GPS log from a bike ride at the bottom of this page