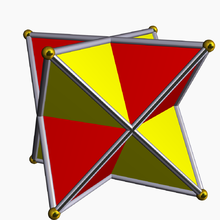
Desmic system

Two desmic tetrahedra. The third tetrahedron of this system is not shown, but has one vertex at the center and the other three on the plane at infinity.

In projective geometry, a desmic system is a set of three tetrahedra in 3-dimensional projective space, such that any two are desmic, (i.e. related such that each edge of one cuts a pair of opposite edges of the other). It was introduced by Stephanos in 1890. The three tetrahedra of a desmic system are contained in a pencil of quartic surfaces. The name "desmic" comes from the Greek word δεσμός, meaning band or chain, referring to the pencil of quartics.

Example

The three tetrahedra given by the equations

• $\displaystyle (w^2-x^2)(y^2-z^2) = 0$
• $\displaystyle (w^2-y^2)(x^2-z^2) = 0$
• $\displaystyle (w^2-z^2)(y^2-x^2) = 0$

form a desmic system, contained in the pencil of quartics

• $\displaystyle a(w^2x^2+y^2z^2) + b(w^2y^2+x^2z^2) + c (w^2z^2+x^2y^2) = 0$

for a + b + c = 0.

References

• Borwein, Peter B (1983), "The Desmic conjecture", Journal of Combinatorial Theory. Series A 35 (1): 1–9, doi:10.1016/0097-3165(83)90022-5, ISSN 1096-0899, MR704251 
• Hudson, R. W. H. T. (1990), Kummer's quartic surface, Cambridge Mathematical Library, Cambridge University Press, ISBN 978-0-521-39790-2, MR1097176, http://www.archive.org/details/184605691 

External links

• Desmic tetrahedra