Denavit–Hartenberg parameters

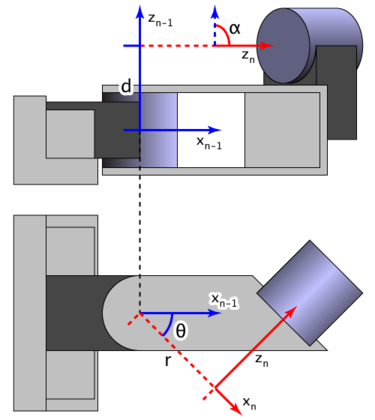
A commonly used convention for selecting frames of reference in robotics applications is the Denavit and Hartenberg (D–H) convention which was introduced by Jaques Denavit and Richard S. Hartenberg. In this convention, each homogeneous transformation is represented as a product of four basic transformations. The common normal between two lines was the main geometric concept that allowed Denavit and Hartenberg to find a minimal representation. The reference frames are laid out as follows:

1. the z-axis is in the direction of the joint axis
2. the x-axis is parallel to the common normal: $x_n = z_n \times z_{n-1}$
   If there is no unique common normal (parallel z axes), then d (below) is a free parameter. The direction of x_n is from z_{n − 1} to z_n, as shown in the video below.
3. the y-axis follows from the x- and z-axis by choosing it to be a right-handed coordinate system.

The transformation is then described by the following four parameters known as D–H parameters:^[1].

• $d\,$: offset along previous z to the common normal
• $\theta\,$: angle about previous z, from old x to new x
• $r\,$: length of the common normal (aka a, but if using this notation, do not confuse with α). Assuming a revolute joint, this is the radius about previous z.
• $\alpha\,$: angle about common normal, from old z axis to new z axis

A visualization of D–H parameterization is available:

• YouTube
• 1280x720 MPEG-4
• 640x360 MPEG-4

There is some choice in frame layout as to whether the previous x axis or the next x points along the common normal. The latter system allows branching chains more efficiently, as multiple frames can all point away from their common ancestor, but in the alternative layout the ancestor can only point toward one successor. Thus the commonly used notation places each down-chain x axis collinear with the common normal, yielding the transformation calculations shown below.

We can note constraints on the relationships between the axes:

• the x_n-axis is perpendicular to both the z_{n − 1} and z_n axes
• the x_n-axis intersects both z_{n − 1} and z_n axes
• the origin of joint n is at the intersection of x_n and z_n
• y_n completes a right-handed reference frame based on x_n and z_n

Every link/joint pair can be described as a coordinate transformation from the previous coordinate system to the next coordinate system.

${}^{n - 1}T_n = \operatorname{Trans}_{z_{n - 1}}(d_n) \cdot \operatorname{Rot}_{z_{n - 1}}(\theta_n) \cdot \operatorname{Trans}_{x_n}(r_n) \cdot \operatorname{Rot}_{x_n}(\alpha_n)$

Note that these are 2 screws after oneanother. See Screw (motion).

The matrices mentioned above are as follows:

$\operatorname{Trans}_{z_{n - 1}}(d_n) = \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & d_n \\ \hline 0 & 0 & 0 & 1 \end{array} \right]$

$\operatorname{Rot}_{z_{n - 1}}(\theta_n) = \left[ \begin{array}{ccc|c} \cos\theta_n & -\sin\theta_n & 0 & 0 \\ \sin\theta_n & \cos\theta_n & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \hline 0 & 0 & 0 & 1 \end{array} \right]$

$\operatorname{Trans}_{x_n}(r_n) = \left[ \begin{array}{ccc|c} 1 & 0 & 0 & r_n \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \hline 0 & 0 & 0 & 1 \end{array} \right]$

$\operatorname{Rot}_{x_n}(\alpha_n) = \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 0 \\ 0 & \cos\alpha_n & -\sin\alpha_n & 0 \\ 0 & \sin\alpha_n & \cos\alpha_n & 0 \\ \hline 0 & 0 & 0 & 1 \end{array} \right]$

This gives:

$\operatorname{}^{n - 1}T_n = \left[ \begin{array}{ccc|c} \cos\theta_n & -\sin\theta_n \cos\alpha_n & \sin\theta_n \sin\alpha_n & r_n \cos\theta_n \\ \sin\theta_n & \cos\theta_n \cos\alpha_n & -\cos\theta_n \sin\alpha_n & r_n \sin\theta_n \\ 0 & \sin\alpha_n & \cos\alpha_n & d_n \\ \hline 0 & 0 & 0 & 1 \end{array} \right] = \left[ \begin{array}{ccc|c} & & & \\ & R & & T \\ & & & \\ \hline 0 & 0 & 0 & 1 \end{array} \right]$

where R is the $3 \times 3$ submatrix describing rotation and T is the $3 \times 1$ submatrix describing translation.

Use of Denavit and Hartenberg matrices

The Denavit and Hartenberg notation gives a standard methodology to write the kinematic equations of a manipulator. This is specially useful for serial manipulators where a matrix is used to represent the pose (position and orientation) of one body with respect to another.

The position of body n with respect to n − 1 may be represented by a position matrix indicated with the symbol T or M

$\operatorname{}^{n - 1}T_n = M_{n-1,n}$

This matrix is also used to transform a point from frame n to n − 1

$P_{(n-1)} = M_{n-1,n} P_{(n)} = \left[ \begin{array}{c} x_{n-1} \\y_{n-1} \\z_{n-1} \\ 1 \end{array} \right] = \left[ \begin{array}{ccc|c} X_x & Y_x & Z_x & T_x \\ X_y & Y_y & Z_y & T_y \\ X_z & Y_z & Z_z & T_z \\ \hline 0 & 0 & 0 & 1 \end{array}\right] \left[ \begin{array}{c} x_{n} \\y_{n} \\z_{n} \\ 1 \end{array} \right]$

Where the upper left $3\times 3$ submatrix of M represents the relative orientation of the two bodies, and the upper right $3\times 1$ represents their relative position.

The position of body k with respect to body i can be obtained as the product of the matrices representing the pose of j with respect of i and that of k with respect of j

M_i,k = M_i,jM_j,k

An important property of Denavit and Hartenberg matrices is

$M_{j,i} = M_{i,j}^{-1}$

Extensions

see ^{[2] [3]}

Kinematics

Further matrices can be defined to represents velocity and acceleration of bodies.

The velocity of body i with respect to body j can be represented in frame k by the matrix

$W_{i,j(k)}=\left[ \begin{array}{ccc|c} 0 & -\omega_z & \omega_y & v_x \\ \omega_z & 0 & -\omega_x & v_y \\ -\omega_y & \omega_x & 0 & v_z \\ \hline 0 & 0 & 0 & 0 \end{array}\right]$

where ω is the angular velocity of body j with respect to body i and all the components are expressed in frame k; v is the velocity of one point of body j with respect to body i (the pole). The pole is the point of j passing through the origin of frame i.

The acceleration matrix can be defined as the sum of the time derivative of the velocity plus the velocity squared

$H_{i,j(k)}=\dot{W}_{i,j(k)}+W_{i,j(k)}^2$

The velocity and the acceleration in frame i of a point of body j can be evaluated as

$\dot{P} = W_{i,j} P$

$\ddot{P} = H_{i,j} P$

It is also possible to prove that

$\dot{M}_{i,j} = W_{i,j(i)} M_{i,j}$

$\ddot{M}_{i,j} = H_{i,j(i)} M_{i,j}$

Velocity and acceleration matrices add up according to the following rules

W_i,k = W_i,j + W_j,k

H_i,k = H_i,j + H_j,k + 2W_i,jW_j,k

in other words the absolute velocity is the sum of the drag plus the relative velocity; for the acceleration the Coriolis' term is also present.

The components of velocity and acceleration matrices are expressed in an arbitrary frame k and transform from one frame to another by the following rule

W_(h) = M_h,kW_(k)M_k,h

H_(h) = M_h,kH_(k)M_k,h

Dynamics

For the dynamics 3 further matrices are necessary to describe the inertia J, the linear and angular momentum Γ, and the forces and torques Φ applied to a body.

Inertia J:

$J=\left[ \begin{array}{ccc|c} I_{xx} & I_{xy} & I_{xz} & x_g m \\ I_{xy} & I_{yy} & I_{yz} & y_g m \\ I_{xz} & I_{yz} & I_{zz} & z_g m \\ \hline x_g m & y_g m & z_g m & m \end{array}\right]$

where m is the mass, $x_g,\, y_g,\, z_g$ represent the position of the center of mass, and the terms $I_{xx},\,I_{xy},\ldots$ represent inertia and are defined as

$I_{xx} =\int\int x^2 \, dm$

$I_{xy} =\int\int xy \, dm$

$I_{xz} =\cdots$

$\cdots$

Action matrix Φ, containing force f and torque t:

$\Phi = \left[ \begin{array}{ccc|c} 0 & -t_z & t_y & f_x \\ t_z & 0 & -t_x & f_y \\ -t_y & t_x & 0 & f_z \\ \hline -f_x & -f_y & -f_z & 0 \end{array}\right]$

Momentum matrix Γ, containing linear ρ and angular γ momentum

$\Phi = \left[ \begin{array}{ccc|c} 0 & -\gamma_z & \gamma_y & \rho_x \\ \gamma_z & 0 & -\gamma_x & \rho_y \\ -\gamma_y & \gamma_x & 0 & \rho_z \\ \hline -\rho_x & -\rho_y & -\rho_z & 0 \end{array}\right]$

the all the matrices are represented with the vector components in a certain frame k. Transformation of the components from frame k to frame h follows to rule

$J_{(h)}= M_{h,k} J_{(k)} M_{h,k}^T$

$\Gamma_{(h)}= M_{h,k} \Gamma_{(k)} M_{h,k}^T$

$\Phi_{(h)}= M_{h,k} \Phi_{(k)} M_{h,k}^T$

The matrices described allow the writing of the dynamic equations in a concise way.

Newton's law:

$\Phi = H J - J H^t \,$

Momentum:

$\Gamma = W J - J W^t \,$

The first of these equations express the Newton's law and is the equivalent of the vector equation f = ma (force equal mass times acceleration) plus $t = J \dot{\omega} + \omega \times J \omega$ (angular acceleration in function of inertia and angular velocity); the second equation permits the evaluation of the linear and angular momentum when velocity and inertia are known.

See also

• Robotics conventions
• J. Denavit and R.S. Hartenberg. A kinematic notation for lower-pair mechanisms based on matrices. Trans ASME J. Appl. Mech, 23:215–221,1955
• R.S. HartenBerg and J. Denavit Kinematic synthesis of linkages McGraw–Hill, New York, NY, 1964
• Giovanni Legnani, Federico Casolo, Paolo Righettini and Bruno Zappa A homogeneous matrix approach to 3D kinematics and dynamics — I. Theory Mechanism and Machine Theory, Volume 31, Issue 5, July 1996, Pages 573–587
• Giovanni Legnani, Federico Casalo, Paolo Righettini and Bruno Zappa A homogeneous matrix approach to 3D kinematics and dynamics—II. Applications to chains of rigid bodies and serial manipulators Mechanism and Machine Theory, Volume 31, Issue 5, July 1996, pages 589–605

References

1. ^ Spong, M., M. Vidyasagar, ”Robot Dynamics and Control”, John Wiley and Sons, 1989, ISBN 047161243X
2. ^ Giovanni Legnani, Federico Casolo, Paolo Righettini and Bruno Zappa ”A homogeneous matrix approach to 3D kinematics and dynamics — I”. Theory Mechanism and Machine Theory, Volume 31, Issue 5, July 1996, Pages 573-587
3. ^ Giovanni Legnani, Federico Casalo, Paolo Righettini and Bruno Zappa ”A homogeneous matrix approach to 3D kinematics and dynamics—II”. Applications to chains of rigid bodies and serial manipulators Mechanism and Machine Theory, Volume 31, Issue 5, July 1996, pages 589–605