- Datar-Mathews Method for Real Option Valuation
-
The Datar-Mathews Method [1] (DM Method ©[2]) is a new method for Real options valuation. The DM Method can be understood as an extension of the net present value (NPV) multi-scenario Monte Carlo model with an adjustment for risk-aversion and economic decision-making. The method uses information that arises naturally in a standard discounted cash flow (DCF), or NPV, project financial valuation. It was created in 2000 by Professor Vinay Datar, Seattle University, and Scott H. Mathews, Technical Fellow, The Boeing Company.
Contents
The Method
The mathematical equation for the DM Method is shown below. The method captures the real option value by discounting the distribution of operating profits at µ, the market risk rate, and discounting the distribution of the discretionary investment at r, risk-free rate, BEFORE the expected payoff is calculated. The option value is then the expected value of the maximum of the difference between the two discounted distributions or zero. Fig. 1.
![C_0 = E_0\left[Max\left(\tilde{S}_te^{-\mu\,\!t}-\tilde{X}_te^{-rt},0\right)\right]](5/be56cedbe0664c089e37339ae624d75c.png)
 is a random variable representing the future benefits, or operating profits. The present valuation of
is a random variable representing the future benefits, or operating profits. The present valuation of  uses μ, a discount rate consistent with the risk level of
uses μ, a discount rate consistent with the risk level of  .
. is a random variable representing the strike price. The present valuation of
is a random variable representing the strike price. The present valuation of  uses r, the rate consistent with the risk of investment,
uses r, the rate consistent with the risk of investment,  . In many generalized option applications, the risk-free discount rate is used. However other discount rates can be considered, such as the corporate bond rate, particularly when the application is a risky corporate product development project.
. In many generalized option applications, the risk-free discount rate is used. However other discount rates can be considered, such as the corporate bond rate, particularly when the application is a risky corporate product development project. is the real option value for a single stage project. The option value can be understood as the expected value of the difference of two present value distributions with an economically rational threshold limiting losses on a risk-adjusted basis.
is the real option value for a single stage project. The option value can be understood as the expected value of the difference of two present value distributions with an economically rational threshold limiting losses on a risk-adjusted basis.
The differential discount rate for μ and r implicitly allows the DM Method to account for the underlying risk. If μ > r, then the option will be risk-averse, typical for both financial and real options. If μ < r, then the option will be risk-seeking. If μ = r, then this is termed a risk-neutral option, and has parallels with NPV-type analyses with decision-making, such as decision trees. The DM Method gives the same results as the Black-Scholes and the binomial lattice option models, provided the same inputs and the discount methods are used. This non-traded real option value therefore is dependent on the risk perception of the evaluator toward the market under assessment relative to privately held investment funds. The DM Method is advantageous for use in real option applications because unlike some other option models it does not require a value for sigma (a measure of uncertainty) or for S0 (the value of the project today), both of which are difficult to derive for new product development projects; see further under Real options valuation. Finally, the DM Method uses real-world values of any distribution type, avoiding the requirement for conversion to risk-neutral values with a lognormal distribution;[3] see further under Monte Carlo methods for option pricing.
Implementation
The method may be implemented using Monte-Carlo simulation, or in a simplified, approximate form.
Using simulation, for each sample, the engine draws a random variable from both
 and
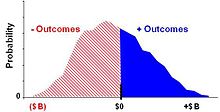
and  , calculates their present values, and takes the difference.[4][5] Fig. 2A. The difference value is compared to zero, the maximum of the two is determined, and the resulting value recorded by the simulation engine. Here, reflecting the optionality inherent in the project, a forecast of a net negative value outcome corresponds to an abandoned project, and has a zero value. Fig. 2B. The resulting values create a payoff distribution representing the economically rational set of plausible, discounted value forecasts of the project at time T0.
, calculates their present values, and takes the difference.[4][5] Fig. 2A. The difference value is compared to zero, the maximum of the two is determined, and the resulting value recorded by the simulation engine. Here, reflecting the optionality inherent in the project, a forecast of a net negative value outcome corresponds to an abandoned project, and has a zero value. Fig. 2B. The resulting values create a payoff distribution representing the economically rational set of plausible, discounted value forecasts of the project at time T0.When sufficient payoff values have been recorded, typically a few hundred, then the mean, or expected value, of the payoff distribution is calculated. Fig. 2C. The option value is the expected value, the first moment of all positive NPVs, of the payoff distribution.
A simple interpretation is:
![Real Option Value = \left[Max\left(Operating Profit\right)-\left(LaunchCosts\right),0)\right]](f/0ff0cebcbdc5363e15564bbdaf3b90cc.png) where Operating Profit and Launch Costs are the appropriately discounted range of cash flows at time 0.[6]
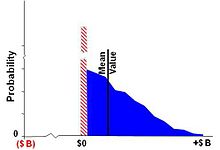
where Operating Profit and Launch Costs are the appropriately discounted range of cash flows at time 0.[6]The sampled distributions may take any form, although the triangular distribution is often used, as is typical for low data situations. Here, the mean value corresponds to the “Most Likely” scenario, typically the same as for the NPV case. Two other scenarios, “Pessimistic” and “Optimistic”, represent plausible deviations from the Most Likely scenario (often modeled as approximating a 1-out-of-20, or 1-out-of-10 likelihood). This range of probabilistic cases tends to be within the organizational memory bounds of the corporation.
An approximate but conservative option value, termed the DM Range Option, can be estimated simply using range estimates of the present values of operating profit and launch costs.[7] Fig. 3. As described, a range is an estimate of a maximum, most-likely (or mode) and minimum (or Optimistic, Most-Likely, Pessimistic) values that circumscribe a triangular distribution. The two distributions are then combined, and, similar to the approach for simulation described, the expected value is the first moment of all positive NPVs. Here, using equations from triangular distributions, the mean of the launch cost distribution is calculated. The present value imputed net profit distribution is the difference between the operating profit distribution and the mean value of the launch cost distribution. In one implementation, the approximate option value is the product of the mean and the probability of the payoff distribution right triangle, the positive value right tail. The DM Range Option requires no simulation. This approach is useful for early-stage estimates of project option value when there has not been sufficient time or resources to gather the necessary quantitative information required for a complete cash flow simulation, or in a portfolio of projects when simulation of all the projects is too computationally demanding.[8] If the launch cost is a scalar value, then the range option value calculation is exact. The range option method is similar to the fuzzy method for real options.
References
- ^ Mathews, S. H., Datar, V. T., and Johnson, B. 2007. A practical method for valuing real options. Journal of Applied Corporate Finance 19(2): 95–104.
- ^ U.S. Patent No. 6,862,579 (issued Mar. 1, 2005). The DM method and related technologies are available for licensing from Boeing.
- ^ Datar, Vinay T. and Mathews, Scott H., 2004. European Real Options: An Intuitive Algorithm for the Black-Scholes Formula. Journal of Applied Finance 14(1): 7-13
- ^ Business Engineering: A Practical Approach to Valuing High-Risk, High-Return Projects Using Real Options Tutorials in Operations Research 2007, Operations Research Tools and Applications: Glimpses of Future Technologies, p157–175
- ^ Business Engineering: A Practical Approach to Valuing High-Risk, High-Return Projects Using Real OptionsINFORMS Annual Meeting, November 4–7, 2007
- ^ Mathews, Scott H., 2009. Tutorial CIFER-T2 Boeing's method for valuing high-risk high-return technology projects using real options. IEEE Symposium on Computational Intelligence for Financial Engineering, 2009.
- ^ Valuing risky projects with real options. Research Technology Management Volume 52 Number 5
- ^ Innovation Portfolio Architecture - Part 2: Attribute Selection and Valuation. Research Technology Management Vol. 54, No. 5 September-October 2011
External links
Categories:- Real options
- Monte Carlo methods in finance
Wikimedia Foundation. 2010.