Conjugate diameters

Two conjugate diameters of an ellipse. Each edge of the bounding parallelogram is parallel to one of the diameters.

In geometry, two diameters of a conic section are said to be conjugate if each chord parallel to one diameter is bisected by the other diameter. For example, two diameters of a circle are conjugate if and only if they are perpendicular.

For an ellipse, two diameters are conjugate if and only if the tangent line to the ellipse at one endpoint of a diameter is parallel to the tangent at the second endpoint. Each pair of conjugate diameters of an ellipse has a corresponding tangent parallelogram, sometimes called the bounding parallelogram. In his manuscript De motu corporum in gyrum, and in the 'Principia', Isaac Newton cites as a lemma proved by previous authors that all (bounding) parallelograms for a given ellipse have the same area.

It is possible to reconstruct an ellipse from any pair of conjugate diameters, or from any bounding parallelogram. For example, in proposition 14 of Book VIII of his Collection, Pappus of Alexandria gives a method for constructing the axes of an ellipse from a given pair of conjugate diameters.

Blue and green hyperbolas are conjugate. A diameter from (x,y) to (−x,−y) is conjugate to the one from (y,x) to (−y,−x).

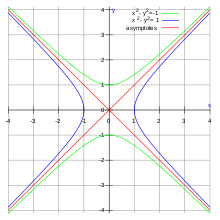
Two hyperbolas are conjugate if they are images of each other in a reflection across an asymptote. A diameter of one hyperbola is conjugate to its reflection in the asymptote, which is a diameter of the other hyperbola. They are hyperbolic-orthogonal to each other.

Conjugate diameters of hyperbolas are useful for stating the principle of relativity in the modern physics of spacetime. The concept of relativity is first introduced in a plane consisting of a single dimension in space, the second dimension being 'time'. In such a plane, one hyperbola corresponds to events a constant distance from the origin event, the other hyperbola corresponds to events a constant proper time from it. The principle of relativity can be formulated "Any pair of conjugate diameters of conjugate hyperbolas can be taken for the axes of space and time". This interpretation of relativity was enunciated by E. T. Whittaker in 1910.

References

• Conjugate Diameters of Ellipse at PlanetMath.
• Conjugate Diameters in Ellipse at cut-the-knot.org.
• William Kingdon Clifford (1878) Elements of Dynamic, page 90, London: MacMillan & Co; on-line presentation by Cornell University Historical Mathematical Monographs.
• George Salmon (1900) A Treatise on Conic Sections, page 165, London: Longmans, Green & Co..
• Whittaker, E.T. (1910), 1. Edition: A History of the theories of aether and electricity, Dublin: Longman, Green and Co. (see page 441)