Infinite broom

In topology, the infinite broom is a subset of the Euclidean plane that is used as an example distinguishing various notions of connectedness. The closed infinite broom is the closure of the infinite broom, and is also referred to as the broom space.^[1]

Definition

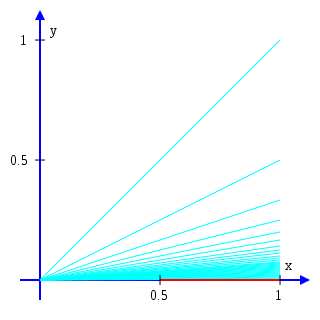
The infinite broom is the subset of the Euclidean plane that consists of all closed line segments joining the origin to the point (1, 1 / n) as n varies over all positive integers, together with the interval (½, 1] on the x-axis.^[2]

The closed infinite broom is then the infinite broom together with the interval (0, ½] on the x-axis. In other words, it consists of all closed line segments joining the origin to the point (1, 1 / n) or to the point (1, 0).^[2]

Properties

Both the infinite broom and its closure are connected, as every open set in the plane which contains the segment on the x-axis must intersect slanted segments. Neither are locally connected. Despite the closed infinite broom being arc connected, the standard infinite broom is not path connected.^[2]

See also

• Comb space

References

1. ^ Chapter 6 exercise 3.5 of Joshi, K. D. (1983), Introduction to general topology, New York: John Wiley & Sons, Inc., ISBN 978-0852264447, MR0709260 
2. ^ ^{a b c} Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978], Counterexamples in Topology (Dover reprint of 1978 ed.), Mineola, NY: Dover Publications, Inc., ISBN 978-0-486-68735-3, MR1382863