- Least common multiple
-
In arithmetic and number theory, the least common multiple (also called the lowest common multiple or smallest common multiple) of two integers a and b, usually denoted by LCM(a, b), is the smallest positive integer that is a multiple of both a and b.[1] It is familiar from grade-school arithmetic as the "lowest common denominator" that must be determined before two fractions can be added.
If either a or b is 0, LCM(a, b) is defined to be zero.
The LCM of more than two integers is also well-defined: it is the smallest number that is an integer multiple of each of them.
Contents
Example
What is the LCM of 4 and 6?
Multiples of 4 are:
- 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76 etc.
and the multiples of 6 are:- 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ...
Common multiples of 4 and 6 are simply the numbers that are in both lists:
- 12, 24, 36, 48, 60, 72, ....
So the least common multiple of 4 and 6 is the smallest one of those: 12
Applications
When adding, subtracting, or comparing vulgar fractions, it is useful to find the least common multiple of the denominators, often called the lowest common denominator, because each of the fractions can be expressed as a fraction with this denominator. For instance,
where the denominator 42 was used because it is the least common multiple of 21 and 6.
Computing the least common multiple
Reduction by the greatest common divisor
The following formula reduces the problem of computing the least common multiple to the problem of computing the greatest common divisor (GCD):
This formula is also valid when exactly one of a and b is 0, since gcd(a, 0) = |a|.
There are fast algorithms for computing the GCD that do not require the numbers to be factored, such as the Euclidean algorithm. To return to the example above,
Because gcd(a, b) is a divisor of both a and b, it's more efficient to compute the LCM by dividing before multiplying:
This reduces the size of one input for both the division and the multiplication, and reduces the required storage needed for intermediate results (overflow in the a×b computation). Because gcd(a, b) is a divisor of both a and b, and thus the division will be guaranteed to yield an integer, so the intermediate result can be stored in an integer. Done this way, the previous example becomes:
Finding least common multiples by prime factorization
The unique factorization theorem says that every positive integer greater than 1 can be written in only one way as a product of prime numbers. The prime numbers can be considered as the atomic elements which, when combined together, make up a composite number.
For example:
Here we have the composite number 90 made up of one atom of the prime number 2, two atoms of the prime number 3 and one atom of the prime number 5.
This knowledge can be used to find the lcm of a set of numbers.
Example: Find the value of lcm(8,9,21).
First, factor out each number and express it as a product of prime number powers.
The lcm will be the product of multiplying the highest power in each prime factor category together. Out of the 4 prime factor categories 2, 3, 5, and 7, the highest powers from each are 23, 32, 50, and 71. Thus,
This method is not as efficient as reducing to the greatest common divisor, since there is no known general efficient algorithm for integer factorization, but is useful in illustrating concepts.
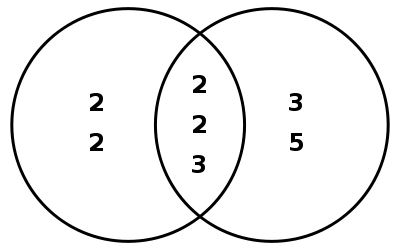
This method can be illustrated using a Venn diagram as follows. Find the prime factorization of each of the two numbers. Put the prime factors into a Venn diagram with one circle for each of the two numbers, and all factors they share in common in the intersection. To find the LCM, just multiply all of the prime numbers in the diagram.
Here is an example:
- 48 = 2 × 2 × 2 × 2 × 3,
- 180 = 2 × 2 × 3 × 3 × 5,
and what they share in common is two "2"s and a "3":
- Least common multiple = 2 × 2 × 2 × 2 × 3 × 3 × 5 = 720
- Greatest common divisor = 2 × 2 × 3 = 12
This also works for the greatest common divisor (GCD), except that instead of multiplying all of the numbers in the Venn diagram, one multiplies only the prime factors that are in the intersection. Thus the GCD of 48 and 180 is 2 × 2 × 3 = 12.
A simple algorithm
This method works as easily for finding the LCM of several integers.
Let there be a finite sequence of positive integers X = (x1, x2, ..., xn), n > 1. The algorithm proceeds in steps as follows: on each step m it examines and updates the sequence X(m) = (x1(m), x2(m), ..., xn(m)), X(1) = X. The purpose of the examination is to pick up the least (perhaps, one of many) element of the sequence X(m). Assuming xk0(m) is the selected element, the sequence X(m+1) is defined as
- xk(m+1) = xk(m), k ≠ k0
- xk0(m+1) = xk0(m) + xk0.
In other words, the least element is increased by the corresponding x whereas the rest of the elements pass from X(m) to X(m+1) unchanged.
The algorithm stops when all elements in sequence X(m) are equal. Their common value L is exactly LCM(X). (For a proof and an interactive simulation see reference below, Algorithm for Computing the LCM.)
A method using a table
This method works for any number of factors. One begins by listing all of the numbers vertically in a table (in this example 4, 7, 12, 21, and 42):
- 4
- 7
- 12
- 21
- 42
The process begins by dividing all of the factors by 2. If any of them divides evenly, write 2 at the top of the table and the result of division by 2 of each factor in the space to the right of each factor and below the 2. If they do not divide evenly, just rewrite the number again. If 2 does not divide evenly into any of the numbers, try 3.
x 2 4 2 7 7 12 6 21 21 42 21 Now, check if 2 divides again:
x 2 2 4 2 1 7 7 7 12 6 3 21 21 21 42 21 21 Once 2 no longer divides, divide by 3. If 3 no longer divides, try 5 and 7. Keep going until all of the numbers have been reduced to 1.
x 2 2 3 7 4 2 1 1 1 7 7 7 7 1 12 6 3 1 1 21 21 21 7 1 42 21 21 7 1 Now, multiply the numbers on the top and you have the LCM. In this case, it is 2 × 2 × 3 × 7 = 84. This is a variation on Euclid's algorithm, as common factors are essentially divided out along the way of dividing all of the numbers at once by each successive factor. You will get to the LCM the quickest if you use prime numbers and start from the lowest prime, 2.
Formulas
Fundamental theorem of arithmetic
According to the fundamental theorem of arithmetic a positive integer is the product of prime numbers, and, except for their order, this representation is unique:
where the exponents n2, n3, ... are non-negative integers; for example, 84 = 22 31 50 71 110 130 ...
Given two integers
 and
and  their least common multiple and greatest common divisor are given by the formulas
their least common multiple and greatest common divisor are given by the formulasand
Since
this gives
In fact, any rational number can be written uniquely as the product of primes if negative exponents are allowed. When this is done, the above formulas remain valid. Using the same examples as above:
Lattice-theoretic
The positive integers may be partially ordered by divisibility: if a divides b (i.e. if b is an integer multiple of a) write a ≤ b (or equivalently, b ≥ a). (Forget the usual magnitude-based definition of ≤ in this section - it isn't used.)
Under this ordering, the positive integers become a lattice with meet given by the gcd and join given by the lcm. The proof is straightforward, if a bit tedious; it amounts to checking that lcm and gcd satisfy the axioms for meet and join. Putting the lcm and gcd into this more general context establishes a duality between them:
- If a formula involving integer variables, gcd, lcm, ≤ and ≥ is true, then the formula obtained by switching gcd with lcm and switching ≥ with ≤ is also true. (Remember ≤ is defined as divides).
The following pairs of dual formulas are special cases of general lattice-theoretic identities.
- Commutative laws


- Idempotent laws

 .
.
It can also be shown[2] that this lattice is distributive, i.e. that lcm distributes over gcd and, dually, that gcd distributes over lcm:
This identitity is self-dual:
Other
Let D be the product of ω(D) distinct prime numbers (i.e. D is squarefree).
Then[3]
where the absolute bars || denote the cardinality of a set.
The LCM in commutative rings
The least common multiple can be defined generally over commutative rings as follows: Let a and b be elements of a commutative ring R. A common multiple of a and b is an element m of R such that both a and b divide m (i.e. there exist elements x and y of R such that ax = m and by = m). A least common multiple of a and b is a common multiple that is minimal in the sense that for any other common multiple n of a and b, m divides n.
In general, two elements in a commutative ring can have no least common multiple or more than one. However, any two least common multiples of the same pair of elements are associates. In a unique factorization domain, any two elements have a least common multiple. In a principal ideal domain, the least common multiple of a and b can be characterised as a generator of the intersection of the ideals generated by a and b (the intersection of a collection of ideals is always an ideal). In principal ideal domains, one can even talk about the least common multiple of arbitrary collections of elements: it is a generator of the intersection of the ideals generated by the elements of the collection.
See also
Notes
References
- Crandall, Richard; Pomerance, Carl (2001), Prime Numbers: A Computatinal Perspective, New York: Springer, ISBN 0-387-04777-9
- Hardy, G. H.; Wright, E. M. (1980), An Introduction to the Theory of Numbers (Fifth edition), Oxford: Oxford University Press, ISBN 978-0198531715
- Landau, Edmund (1966), Elementary Number Theory, New York: Chelsea
External links
Categories:
Wikimedia Foundation. 2010.