Clique-sum

A clique-sum of two planar graphs and the Wagner graph, forming a K₅-free graph.

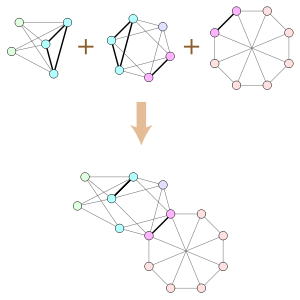
In graph theory, a branch of mathematics, a clique-sum is a way of combining two graphs by gluing them together at a clique, analogous to the connected sum operation in topology. If two graphs G and H each contain cliques of equal size, the clique-sum of G and H is formed from their disjoint union by identifying pairs of vertices in these two cliques to form a single shared clique, and then possibly deleting some of the clique edges. A k-clique-sum is a clique-sum in which both cliques have at most k vertices. One may also form clique-sums and k-clique-sums of more than two graphs, by repeated application of the two-graph clique-sum operation.

Related concepts

Clique-sums have a close connection with treewidth: If two graphs have treewidth at most k, so does their k-clique-sum. Every tree is the 1-clique-sum of its edges. Every series-parallel graph, or more generally every graph with treewidth at most two, may be formed as a 2-clique-sum of triangles. The same type of result extends to larger values of k: every graph with treewidth at most k may be formed as a clique-sum of graphs with at most k + 1 vertices; this is necessarily a k-clique-sum.^[1]

There is also a close connection between clique-sums and graph connectivity: if a graph is not (k + 1)-vertex-connected (so that there exists a set of k vertices the removal of which disconnects the graph) then it may be represented as a k-clique-sum of smaller graphs. For instance, the SPQR tree of a biconnected graph is a representation of the graph as a 2-clique-sum of its triconnected components.

Application in graph structure theory

Clique-sums are important in graph structure theory, where they are used to characterize certain families of graphs as the graphs formed by clique-sums of simpler graphs. The first result of this type^[2] was a theorem of Wagner (1937), who proved that the graphs that do not have a five-vertex complete graph as a minor are the 3-clique-sums of planar graphs with the eight-vertex Wagner graph; this structure theorem can be used to show that the four color theorem is equivalent to the case k = 5 of the Hadwiger conjecture. The chordal graphs are exactly the graphs that can be formed by clique-sums of cliques without deleting any edges.^[3] The graphs in which every induced cycle of length four or greater forms a minimal separator of the graph (its removal partitions the graph into two or more disconnected components, and no subset of the cycle has the same property) are exactly the clique-sums of cliques and maximal planar graphs, again without edge deletions.^[4] Johnson & McKee (1996) use the clique-sums of chordal graphs and series-parallel graphs to characterize the partial matrices having positive definite completions.

It is possible to derive a clique-sum decomposition for any graph family closed under graph minor operations: the graphs in every minor-closed family may be formed from clique-sums of graphs that are "nearly embedded" on surfaces of bounded genus, meaning that the embedding is allowed to omit a small number of apexes (vertices that may be connected to an arbitrary subset of the other vertices) and vortices (graphs with low pathwidth that replace faces of the surface embedding).^[5] These characterizations have been used as an important tool in the construction of approximation algorithms and subexponential-time exact algorithms for NP-complete optimization problems on minor-closed graph families.^[6]

Generalizations

The theory of clique-sums may also be generalized from graphs to matroids.^[1] Notably, Seymour's decomposition theorem characterizes the regular matroids (the matroids representable by totally unimodular matrices) as the 3-sums of graphic matroids (the matroids representing spanning trees in a graph), cographic matroids, and a certain 10-element matroid.^[1][7]

Notes

1. ^ ^{a b c} Lovász (2006).
2. ^ As credited by Kříž & Thomas (1990), who list several additional clique-sum-based characterizations of graph families.
3. ^ Seymour & Weaver (1984).
4. ^ Diestel (1987).
5. ^ Robertson & Seymour (2003)
6. ^ Demaine et al. (2004); Demaine et al. (2005); Demaine, Hajiaghayi & Kawarabayashi (2005).
7. ^ Seymour (1980).

References

• Demaine, Erik D.; Fomin, Fedor V.; Hajiaghayi, MohammedTaghi; Thilikos, Dimitrios (2005), "Subexponential parameterized algorithms on bounded-genus graphs and H-minor-free graphs", Journal of the ACM 52 (6): 866–893, doi:10.1145/1101821.1101823, MR2179550 .
• Demaine, Erik D.; Hajiaghayi, MohammedTaghi; Nishimura, Naomi; Ragde, Prabhakar; Thilikos, Dimitrios (2004), "Approximation algorithms for classes of graphs excluding single-crossing graphs as minors", Journal of Computing and Systems Sciences 69 (2): 166–195, doi:10.1016/j.jcss.2003.12.001, MR2077379 .
• Demaine, Erik D.; Hajiaghayi, MohammedTaghi; Kawarabayashi, Ken-ichi (2005), "Algorithmic graph minor theory: decomposition, approximation, and coloring" (PDF), Proc. 46th IEEE Symp. Foundations of Computer Science, pp. 637–646, doi:10.1109/SFCS.2005.14, http://www-math.mit.edu/~hajiagha/graphminoralgorithm.pdf .
• Diestel, Reinhard (1987), "A separation property of planar triangulations", Journal of Graph Theory 11 (1): 43–52, doi:10.1002/jgt.3190110108, MR876203 .
• Kříž, Igor; Thomas, Robin (1990), "Clique-sums, tree-decompositions and compactness", Discrete Mathematics 81 (2): 177–185, doi:10.1016/0012-365X(90)90150-G, MR1054976 .
• Johnson, Charles R.; McKee, Terry A. (1996), "Structural conditions for cycle completable graphs", Discrete Mathematics 159 (1–3): 155–160, doi:10.1016/0012-365X(95)00107-8, MR1415290 .
• Lovász, László (2006), "Graph minor theory", Bulletin of the American Mathematical Society 43 (1): 75–86, doi:10.1090/S0273-0979-05-01088-8, MR2188176 .
• Robertson, N.; Seymour, P. D. (2003), "Graph minors XVI. Excluding a non-planar graph", Journal of Combinatorial Theory, Series B 89 (1): 43–76, doi:10.1016/S0095-8956(03)00042-X, MR1999736 .
• Seymour, P. D. (1980), "Decomposition of regular matroids", Journal of Combinatorial Theory, Series B 28 (3): 305–359, doi:10.1016/0095-8956(80)90075-1, MR0579077 .
• Seymour, P. D.; Weaver, R. W. (1984), "A generalization of chordal graphs", Journal of Graph Theory 8 (2): 241–251, doi:10.1002/jgt.3190080206, MR0742878 .
• Wagner, Klaus (1937), "Über eine Eigenschaft der ebenen Komplexe", Mathematische Annalen 114: 570–590, doi:10.1007/BF01594196 .