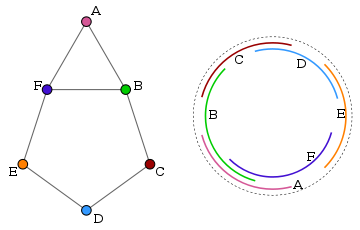
Circular-arc graph

A circular-arc graph (left) and a corresponding arc model (right).

In graph theory, a circular-arc graph is the intersection graph of a set of arcs on the circle. It has one vertex for each arc in the set, and an edge between every pair of vertices corresponding to arcs that intersect.

Formally, let

$I_1, I_2, \ldots, I_n \subset C_1$

be a set of arcs. Then the corresponding circular-arc graph is G = (V, E) where

$V = \{I_1, I_2, \ldots, I_n\}$

and

$\{I_\alpha, I_\beta\} \in E \iff I_\alpha \cap I_\beta \neq \varnothing.$

A family of arcs that corresponds to G is called an arc model.

Recognition

Tucker (1980) demonstrated the first polynomial recognition algorithm for circular-arc graphs, which runs in ${\mathcal O}(n^3)$ time. More recently, McConnell (2003) gave the first linear $({\mathcal O}(n+m))$ time recognition algorithm.

Relation to other graph classes

Circular-arc graphs are a natural generalization of interval graphs. If a circular-arc graph G has an arc model that leaves some point of the circle uncovered, the circle can be cut at that point and stretched to a line, which results in an interval representation. Unlike interval graphs, however, circular-arc graphs are not always perfect, as the odd chordless cycles C₅, C₇, etc., are circular-arc graphs.

Some subclasses

In the following, let G = (V,E) be an arbitrary graph.

Unit circular-arc graphs

G is a unit circular-arc graph if there exists a corresponding arc model such that each arc is of equal length.

Proper circular-arc graphs

G is a proper circular-arc graph (also known as a circular interval graph ^[1]) if there exists a corresponding arc model such that no arc properly contains another. Recognizing these graphs and constructing a proper arc model can both be performed in linear $({\mathcal O}(n + m))$ time.^[2]

Helly circular-arc graphs

G is a Helly circular-arc graph if there exists a corresponding arc model such that the arcs constitute a Helly family. Gavril (1974) gives a characterization of this class that implies an ${\mathcal O(n^3)}$ recognition algorithm.

Joeris et al. (2009) give other characterizations (including one by forbidden induced subgraphs) of this class, which imply a recognition algorithm that runs in O(n+m) time when the input is a graph. If the input graph is not a Helly circular-arc graph, then the algorithm returns a certificate of this fact in the form of a forbidden induced subgraph. They also gave an O(n) time algorithm for determining whether a given circular-arc model has the Helly property.

Applications

Circular-arc graphs are useful in modeling periodic resource allocation problems in operations research. Each interval represents a request for a resource for a specific period repeated in time.

Notes

1. ^ Chudnovsky & Seymour (2008) pg. ?
2. ^ Deng, Hell & Huang (1996) pg. ?

References

• Joeris, Benson L.; Lin, Min Chih; McConnell, Ross M.; Spinrad, Jeremy P.; Szwarcfiter, Jayme L. (2009), "Linear-Time Recognition of Helly Circular-Arc Models and Graphs", Algorithmica 59 (2): 215–239, doi:10.1007/s00453-009-9304-5 .

• Tucker, Alan (1980), "An efficient test for circular-arc graphs", SIAM Journal on Computing 9 (1): 1–24, doi:10.1137/0209001 .

• McConnell, Ross (2003), "Linear-time recognition of circular-arc graphs", Algorithmica 37 (2): 93–147, doi:10.1007/s00453-003-1032-7 

• Golumbic, Martin Charles (1980), Algorithmic Graph Theory and Perfect Graphs, Academic Press, ISBN 0-444-51530-5, http://www.elsevier.com/wps/find/bookdescription.cws_home/699916/description#description  Second edition, Annals of Discrete Mathematics 57, Elsevier, 2004.

• Deng, Xiaotie; Hell, Pavol; Huang, Jing (1996), "Linear-Time representation algorithms for proper circular-arc graphs and proper interval graphs", SIAM Journal on Computing 25 (2): 390–403, doi:10.1137/S0097539792269095 .

• Gavril, Fanica (1974), "Algorithms on circular-arc graphs", Networks 4 (4): 357–369, doi:10.1002/net.3230040407 

External links

• "circular arc graph". Information System on Graph Class Inclusions. http://wwwteo.informatik.uni-rostock.de/isgci/classes/gc_133.html.