- Marden's theorem
-
A triangle and its Steiner inellipse. The zeroes of p(z) are the black dots, and the zeroes of p'(z) are the red dots). The center green dot is the zero of p"(z). Marden's theorem states that the red dots are the foci of the ellipse.
In mathematics, Marden's theorem, named after Morris Marden, gives a geometric relationship between the zeroes of a third-degree polynomial with complex coefficients and the zeroes of its derivative.
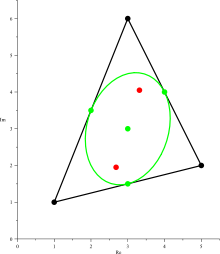
A cubic polynomial has three zeroes in the complex number plane, which in general form a triangle, and the Gauss–Lucas theorem states that the roots of its derivative lie within this triangle. Marden's theorem states their location within this triangle more precisely:
- Suppose the zeroes z1, z2, and z3 of a third-degree polynomial p(z) are non-collinear. There is a unique ellipse inscribed in the triangle with vertices z1, z2, z3 and tangent to the sides at their midpoints: the Steiner inellipse. The foci of that ellipse are the zeroes of the derivative p'(z).
By the Gauss–Lucas theorem, the root of the double derivative p"(z) must be the average of the two foci, which is the center point of the ellipse and the centroid of the triangle. In the special case that the triangle is equilateral (as happens, for instance, for the polynomial p(z) = z3 − 1) the inscribed ellipse degenerates to a circle, and the derivative of p has a double root at the center of the circle. Conversely, if the derivative has a double root, then the triangle must be equilateral (Kalman 2008a).
A more general version of the theorem, due to Linfield (1920), applies to polynomials p(z) = (z − a)i (z − b)j (z − c)k whose degree i + j + k may be higher than three, but that have only three roots a, b, and c. For such polynomials, the roots of the derivative may be found at the multiple roots of the given polynomial (the roots whose exponent is greater than one) and at the foci of an ellipse whose points of tangency to the triangle divide its sides in the ratios i : j, j : k, and k : i.
Marden (1945, 1966) attributes what is now known as Marden's theorem to Siebeck (1864) and cites nine papers that included a version of the theorem. Dan Kalman won the 2009 Lester R. Ford Award of the Mathematical Association of America for his 2008 paper in the American Mathematical Monthly describing the theorem.
References
- Kalman, Dan (2008a), "An Elementary Proof of Marden's Theorem", The American Mathematical Monthly 115: 330–338, ISSN 0002-9890, http://mathdl.maa.org/mathDL/22/?pa=content&sa=viewDocument&nodeId=3338&pf=1
- Kalman, Dan (2008b), "The Most Marvelous Theorem in Mathematics", Journal of Online Mathematics and its Applications, http://mathdl.maa.org/mathDL/4/?pa=content&sa=viewDocument&nodeId=1663
- Linfield, B. Z. (1920), "On the relation of the roots and poles of a rational function to the roots of its derivative", Bulletin of the American Mathematical Society 27: 17–21, doi:10.1090/S0002-9904-1920-03350-1.
- Marden, Morris (1945), "A note on the zeroes of the sections of a partial fraction", Bulletin of the American Mathematical Society 51 (12): 935–940, doi:10.1090/S0002-9904-1945-08470-5, http://www.ams.org/bull/1945-51-12/S0002-9904-1945-08470-5/home.html
- Marden, Morris (1966), Geometry of Polynomials, Mathematical Surveys, 3, Providence, R.I.: American Mathematical Society
- Siebeck, Jörg (1864), "Über eine neue analytische Behandlungweise der Brennpunkte", Journal für die reine und angewandte Mathematik 64: 175–182, ISSN 0075-4102, http://gdz.sub.uni-goettingen.de/dms/load/img/?PPN=GDZPPN002152495
Categories:- Triangles
- Polynomials
- Conic sections
- Theorems in geometry
Wikimedia Foundation. 2010.
