Bundle adjustment

---

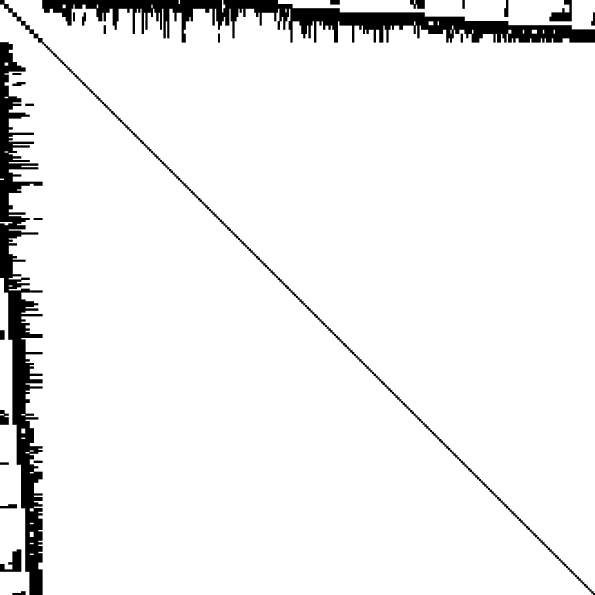
right|thumb|A sparse matrix obtained when solving a modestlysized bundle adjustment problem. This is the sparsity pattern of a 992x992 normal equations(i.e. approximate Hessian) matrix. Black regions correspond to nonzero blocks.Given a set of images depicting a number of 3D points from different viewpoints,bundle adjustment can be defined as the problem of simultaneously refining the 3D
coordinates describing the scene geometry as well as the parameters ofthe relative motion and the optical characteristics of the camera(s) employed to acquire theimages, according to an optimality criterion involving the correspondingimage projections of all points.

Bundle adjustment is almost always used as the last step of every feature-based 3D reconstruction algorithm.It amounts to an optimization problem on the 3D structure and viewing parameters (i.e., camera
pose and possibly intrinsic calibration and radial distortion),to obtain a reconstruction which is optimal under certain assumptions regarding the noisepertaining to the observed image features: If the image error is zero-mean Gaussian,then bundle adjustment is the Maximum Likelihood Estimator. Its name refersto the "bundles" of light rays originating from each 3D feature and converging on each camera'soptical center, which are adjusted optimally with respect to both the structure and viewing parameters.Bundle adjustment was originally conceived in the field of photogrammetry during 1950s andhas increasingly been used by computer vision researchers during recent years.

Bundle adjustment boils down to minimizing the reprojection error between the image locations of observed and predicted image points, which is expressed as the sum of squares of a large number ofnonlinear, real-valued functions. Thus, the minimization is achieved using nonlinear least-squares algorithms,from which Levenberg-Marquardt has proven to be one of the most successful due to its ease of implementationand its use of an effective damping strategy that lends it the ability to converge quickly from awide range of initial guesses.By iteratively linearizing the function to be minimized in the neighborhood of the current estimate,the Levenberg-Marquardt algorithm involves the solution of linear systems known as the normal equations. When solving the minimization problems arising in the framework of bundle adjustment, the normal equationshave a sparse block structure owing to the lack of interaction among parameters for different3D points and cameras. This can be exploited to gain tremendous computational benefits by employing a sparsevariant of the Levenberg-Marquardt algorithm which explicitly takes advantage of the normal equationszeros pattern, avoiding storing and operating on zero elements.

Mathematical definition

Bundle adjustment amounts to jointly refining a set of initial camera and structure parameter estimatesfor finding the set of parameters that most accurately predict the locations of the observed points inthe set of available images. More formally, assume that $n$ 3D points are seen in $m$views and let $mathbf\{x\}\_\{ij\}$ be the projection of the $i$-th point on image$j$. Let $displaystyle\; v\_\{ij\}$ denote the binary variables that equal 1 if point$i$ is visible in image $j$ and 0 otherwise. Assume also that each camera$j$ is parameterized by a vector $mathbf\{a\}\_j$ and each 3D point $i$by a vector $mathbf\{b\}\_i$. Bundle adjustment minimizes the total reprojection error withrespect to all 3D point and camera parameters, specifically

:$min\_\{mathbf\{a\}\_j,\; ,\; mathbf\{b\}\_i\}\; displaystylesum\_\{i=1\}^\{n\}\; ;\; displaystylesum\_\{j=1\}^\{m\}\; ;\; v\_\{ij\}\; ,\; d(mathbf\{Q\}(mathbf\{a\}\_j,\; ,\; mathbf\{b\}\_i),\; ;\; mathbf\{x\}\_\{ij\})^2,$

where $mathbf\{Q\}(mathbf\{a\}\_j,\; ,\; mathbf\{b\}\_i)$ is the predicted projectionof point $i$ on image $j$ and $d(mathbf\{x\},\; ,\; mathbf\{y\})$denotes the Euclidean distance between the image points represented by vectors $mathbf\{x\}$and $mathbf\{y\}$. Clearly, bundle adjustment is by definition tolerant to missing imageprojections and minimizes a physically meaningful criterion.

References

* cite conference
title=Bundle Adjustment — A Modern Synthesis
author=B. Triggs
coauthors=P. McLauchlan and R. Hartley and A. Fitzgibbon
booktitle=ICCV '99: Proceedings of the International Workshop on Vision Algorithms
pages=298-372 | id=ISBN 3-540-67973-1
publisher=Springer-Verlag
year=1999

*cite book
author=R.I. Hartley and A. Zisserman
title=Multiple View Geometry in computer vision
publisher=Cambridge University Press
edition=2nd ed.
year=2004
id=ISBN 0521540518

ee also

*Photogrammetry
*Stereoscopy
*Levenberg-Marquardt algorithm
*Sparse matrix

External links

* [http://lear.inrialpes.fr/pubs/2000/TMHF00/Triggs-va99.pdf B. Triggs, P. McLauchlan, R. Hartley and A. Fitzgibbon, "Bundle Adjustment — A Modern Synthesis", Vision Algorithms: Theory and Practice, 1999]
* [http://www.ics.forth.gr/~lourakis/sba/ M. Lourakis, "sba: A Generic Sparse Bundle Adjustment C/C++ Package Based on the Levenberg-Marquardt Algorithm", 2004]