Domino problem

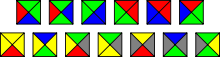An aperiodic set of Wang dominoes.^[1]

In geometry, the domino problem is the problem of deciding whether a set of tiles of a particular kind admits a tiling.

In a 1961 paper^[2] proposing a method for deciding an important case of David Hilbert's Entscheidungsproblem, the logician Hao Wang discussed tiling the plane by equally sized square plates with colored edges, now called Wang tiles or Wang dominoes. A domino set is a finite set of such plates that may not be rotated or reflected, each colored in a different way. A domino set is solvable if an infinite plane, ruled by squares of the same size as the dominoes, can be covered by copies of dominoes in the set, with a domino on each square, in such a way that colors on adjacent domino edges match.^[3]

According to Wang's student, Robert Berger,^[4]

The Domino Problem deals with the class of all domino sets. It consists of deciding, for each domino set, whether or not it is solvable. We say that the Domino Problem is decidable or undecidable according to whether there exists or does not exist an algorithm which, given the specifications of an arbitrary domino set, will decide whether or not the set is solvable.

In other words, is there an effective procedure for settling the problem for any given domino set?

Wang made the following

Fundamental Conjecture: A finite set of plates is solvable if and only if there exists a cyclic rectangle of the plates; or in other words, a finite set of plates is solvable if and only if it has at least one periodic solution.^[2]

In short, he conjectured that there is no aperiodic domino set. Wang observed that if this conjecture is true, then the Domino Problem is decidable. If every domino set either does not admit a tiling, or admits a periodic tiling, then there is an algorithm for deciding which is the case: enumerate all possible coverings of larger and larger rectangles until either there is some size of rectangle that the tiles cannot cover, or until a fundamental domain for a periodic tiling is found. Either way, the algorithm will eventually halt, so long as no aperiodic set exists.

This observation holds in a wide range of settings, such as tiling by unmarked polygons: if there is no aperiodic set, it suffices to enumerate all possible configurations of any given set of tiles and check whether the configuration is a fundamental domain for some periodic tiling.

In 1966, Berger proved the Domino Problem is undecidable for Wang dominoes (and implicitly, for planar tiles in general),^[3] incidentally giving an aperiodic set of over 20,000 Wang dominoes. (In his unpublished Ph.D. thesis, he gives a smaller set of 104.)

Raphael Robinson reworked Berger's proof in 1971 paper and provided a smaller domino set.^[5]

References

1. ^ Culik, Karel; Kari, Jarkko (1997), On aperiodic sets of Wang tiles, Lecture Notes in Computer Science, 1337, pp. 153–162, doi:10.1007/BFb0052084 .
2. ^ ^{a b} Wang, Hao (1961), "Proving theorems by pattern recognition II", Bell System Technical Journal 40: 1–42 .
3. ^ ^{a b} Berger, Robert (1966), "The undecidability of the Domino Problem", Memoirs of the American Mathematical Society 66 .
4. ^ Berger 1966, page 2.
5. ^ Robinson, R.M. (1971), "Undecidability and nonperiodicity for tilings of the plane", Inventiones Mathematicae 12 (3): 177–209, doi:10.1007/BF01418780 .

• Grünbaum, Branko; Shephard, G. C. (1987), Tilings and Patterns, New York: W. H. Freeman, ISBN 978-716711933 .