Transversal (geometry)

A transversal cutting two parallel lines

In geometry, a transversal is a line that passes through two or more other lines in the same plane at different points. When the lines are parallel, as is often the case, a transversal produces several congruent and several supplementary angles. When three lines in general position that form a triangle are cut by a transversal, the lengths of the six resulting segments satisfy Menelaus' theorem.

Terminology

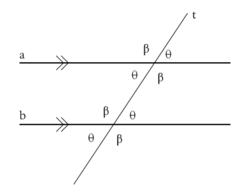
Alternate exterior angles created by a transversal of two lines.		Alternate interior angles created by a transversal of two lines.

When a line l is the transversal of two lines m and n there are a total of eight angles formed. Names have been given to these angles and specific pairs. There are four interior angles defined as angles between m and n, and the remaining four are called exterior angles. A pair of angles, one formed by l and m and the other formed by l and n, are called corresponding angles if they are on the same side of l and on the same sides of m and n respectively. Similarly, a pair of angles are called alternating angles if they are on opposite sides of l and opposite sides of m and n.^[1]

Related Theorems

Euclid's formulation of the parallel postulate may stated in terms of a transversal. Specifically, if the interior angles on the same side of the transversal are less than two right angles then lines must intersect. In fact, Euclid uses the same phrase in Greek that is usually translated as "transversal".^[2]

Euclid's Proposition 27 states that if a transversal intersects two lines so that alternate interior angles are congruent, then the lines are parallel. Euclid proves this by contradiction: If the lines are not parallel then they must intersect and a triangle is formed. Then one of the alternate angles is an exterior angle equal to the other angle which is an opposite interior angle in the triangle. This contradicts Proposition 16 which states that an exterior angle on a triangle is always greater than the opposite interior angles.^[3][4]

Euclid's Proposition 28 extends this result in two ways. First, if a transversal intersects two lines so that corresponding angles are congruent, then the lines are parallel. Second, if a transversal intersects two lines so that interior angles on the same side of the transversal are supplementary, then the lines are parallel. These follow from the previous proposition by applying the fact than opposite angles on intersecting lines equal (Prop. 15) and that adjacent angles on a line are supplementary (Prop. 13). As noted by Proclus, Euclid gives only three of a possible six such criteria for parallel lines.^[5][6]

Euclid's Proposition 29 is a converse to the previous two. First, if a transversal intersects two parallel lines, then the alternate interior angles are congruent. If not then one is greater than the other, which implies it's supplement is less than the supplement of the other angle. This implies that there are interior angles on the same side of the transversal which are less than two right angles, contradicting the fifth postulate. The proposition continues by stating that in a transversal of two parallel lines, corresponding angles are congruent and interior angles on the same side equal two right angles. These statements follow in the same way that Prop. 28 follows from Prop. 27.^[7][8]

Euclid's proof makes essential use of fifth postulate, however modern treatments of geometry use Playfair's axiom instead. To prove proposition 29 assuming Playfair's axiom, let a transversal cross two parallel lines and suppose alternate interior angles are not equal. Draw a third line through the point where the transversal crosses the first line, but with angle equal to the angle the transversal makes with the second angle. This produces two different lines through a point both parallel to another line, contradicting the axiom.^[9][10]

External links

• Transversal and Angles Interactive transversal with color coded angles (corresponding, alternate interior etc..)
• Transversal definition With interactive animation
• The alternate interior angles associated with a transversal With interactive animation
• The alternate exterior angles associated with a transversal With interactive animation
• Corresponding angles associated with a transversal line With interactive animations
• Exterior angles associated with a transversal line With interactive animation

References

1. ^ Holgate art. 87
2. ^ Heath p. 308 note 1
3. ^ Heath p. 307
4. ^ See also Holgate Art. 88
5. ^ Heath p. 309-310
6. ^ See also Holgate Art. 89-90
7. ^ Heath p. 311-312
8. ^ See also Holgate Art. 93-95
9. ^ Heath p. 313
10. ^ A similar proof is given in Holgate Art. 93

• Holgate, Thomas Franklin (1901). Elementary Geometry. Macmillan. 
• Thomas Little Heath, T.L. (1908). The thirteen books of Euclid's Elements. 1. The University Press. pp. 307 ff..