- Compass equivalence theorem
-
The compass equivalence theorem is an important statement in compass and straightedge constructions. In these constructions it is assumed that whenever a compass is lifted from a page, it collapses, so that it may not be directly used to transfer distances. While this might seem a difficult obstacle to surmount, the compass equivalence theorem states that any construction via a "fixed" compass may be attained with a collapsing compass. In other words, it is possible to construct a circle of equal radius, centered at any given point on the plane. This theorem is known as Proposition II of Book I of Euclid's Elements.
Proof
We are given points A, B, and C, and wish to construct a circle centered at A with the same radius as BC (the first green circle).
- Draw a circle centered at A and passing through B and vice versa (the red circles). They will intersect at point D and form equilateral triangle ABD.
- Extend DB past B and find the intersection of DB and the circle BC, labeled E.
- Create a Circle centered at D and passing through E (the blue circle).
- Extend DA past A and find the Intersection of the DA and the circle DE, labeled F.
- Construct a circle centered at A and passing through F (the second green circle)
- Because E is on the circle BC, BE=BC.
- Because ADB is an equilateral triangle, DA=DB.
- Because E and F are on a circle around D, DE=DF.
- Therefore, AF=BE and AF=BC.
Alternate Proof without Straightedge
It is possible to prove compass equivalence without the use of the straightedge. This justifies the use of "fixed compass" moves in proofs of the Mohr-Mascheroni theorem, which states that any construction possible with straightedge and compass can be accomplished with compass alone.
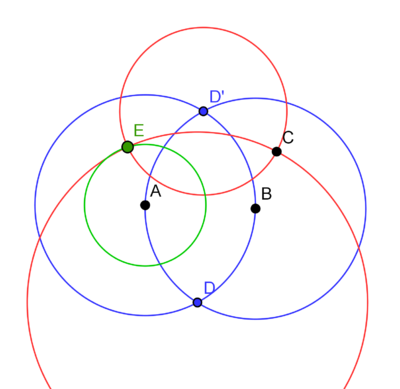
We are given points A, B, and C, and wish to construct a circle centered at A with the same radius as BC, using only a collapsing compass and no straightedge.
- Draw a circle centered at A and passing through B and vice versa (the blue circles). They will intersect at points D and D'.
- Now draw circles through C with centers at D and D' (the red circles). Find their other intersection and label it E.
- Draw a circle (the green circle) with center A passing through E.
- The line DD' is the perpendicular bisector of AB. Thus A is the reflection of B through line DD'.
- By construction, E is the reflection of C through line DD'.
- Since reflection is an isometry, it follows that AE=BC as desired.
External links
Categories:- Euclidean plane geometry
Wikimedia Foundation. 2010.