Hidden Markov model

---

right|thumb|300px">
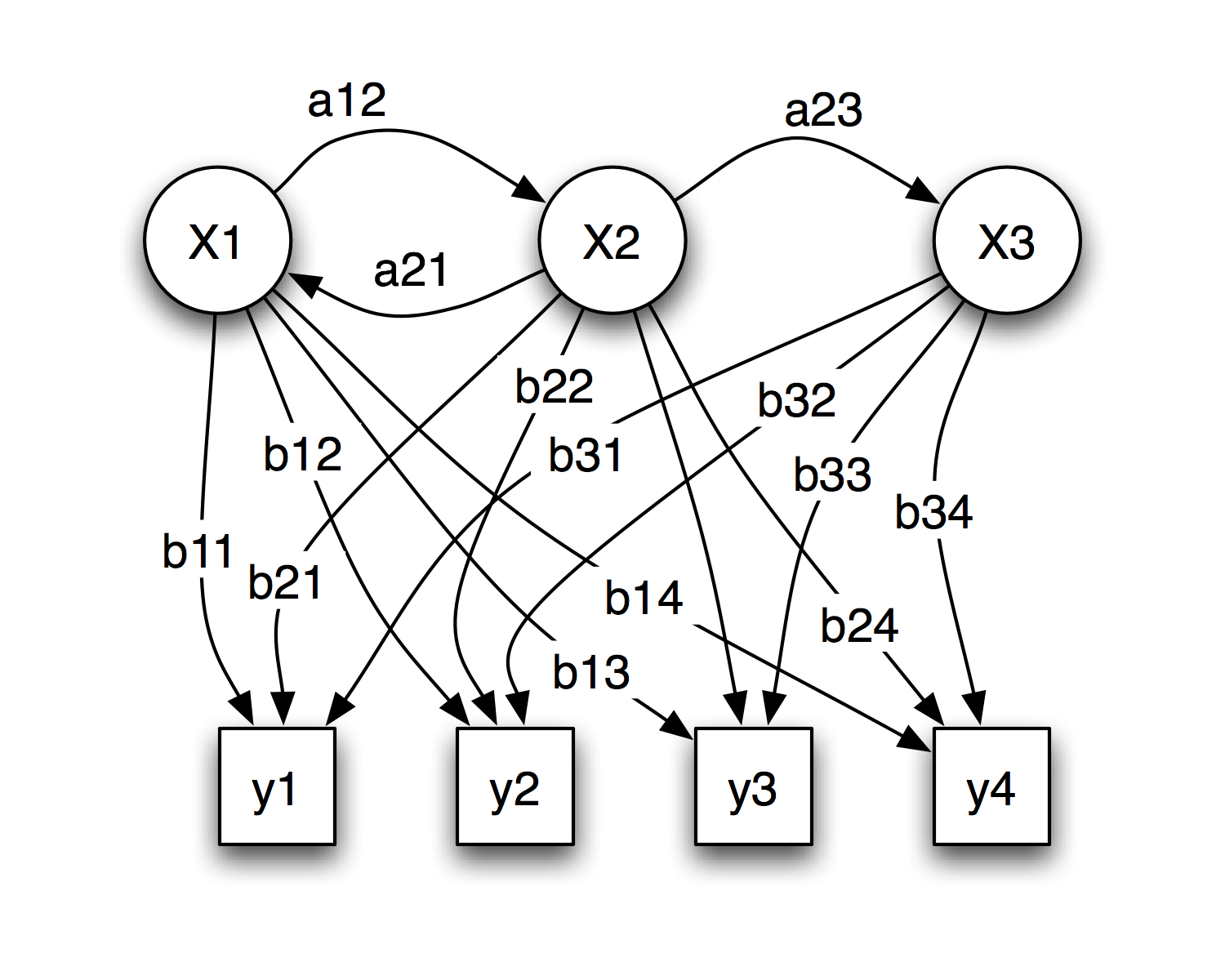
Probabilistic parameters of a hidden Markov model (example)
"x" — states
"y" — possible observations
"a" — state transition probabilities
"b" — output probabilitiesA hidden Markov model (HMM) is a statistical model in which the system being modeled is assumed to be a Markov process with unknown parameters, and the challenge is to determine the hidden parameters from the observable parameters. The extracted model parameters can then be used to perform further analysis, for example for pattern recognition applications. An HMM can be considered as the simplest dynamic Bayesian network.

In a regular Markov model, the state is directly visible to the observer, and therefore the state transition probabilities are the only parameters. In a "hidden" Markov model, the state is not directly visible, but variables influenced by the state are visible. Each state has a probability distribution over the possible output tokens. Therefore the sequence of tokens generated by an HMM gives some information about the sequence of states.

Hidden Markov models are especially known for their application in temporal pattern recognition such as speech, handwriting, gesture recognition, part-of-speech tagging, musical score following, partial discharges and bioinformatics.

Architecture of a hidden Markov model

The diagram below shows the general architecture of an instantiated HMM. Each oval shape represents a random variable that can adopt a number of values. The random variable $x(t)$ is the hidden state at time $t$ (with the model from the above diagram, $x(t)\; in\; \{x\_1,\; x\_2,\; x\_3\}$). The random variable $y(t)$ is the observation at time $t$ ($y(t)\; in\; \{y\_1,\; y\_2,\; y\_3,\; y\_4\}$). The arrows in the diagram (often called a trellis diagram) denote conditional dependencies.

From the diagram, it is clear that the value of the hidden variable $x(t)$ (at time $t$) "only" depends on the value of the hidden variable $x(t-1)$ : the values at time $t-2$ and before have no influence. This is called the Markov property. Similarly, the value of the observed variable $y(t)$ only depends on the value of the hidden variable $x(t)$ (both at time $t$).

Probability of an observed sequence

5 3 2 5 3 2
5 3 1 2 1 2
4 3 2 5 3 2
4 3 1 2 1 2
3 1 2 5 3 2
Transition and observation probabilities are indicated by the line opacity.The probability of observing a sequence $Y=y(0),\; y(1),dots,y(L-1)$ of length $L$ is given by

:$P(Y)=sum\_\{X\}P(Ymid\; X)P(X),$

where the sum runs over all possible hidden node sequences $X=x(0),\; x(1),\; dots,\; x(L-1)$. Brute force calculation of $P(Y)$ is intractable for most real-life problems, as the number of possible hidden node sequences is typically extremely high. The calculation can however be sped up enormously using the forward algorithm [Rabiner, p. 262] or the equivalent backward algorithm.

Using hidden Markov models

There are three canonical problems associated with HMM:
* Given the parameters of the model, compute the probability of a particular output sequence, and the probabilities of the hidden state values given that output sequence. This problem is solved by the forward-backward algorithm.
* Given the parameters of the model, find the most likely sequence of hidden states that could have generated a given output sequence. This problem is solved by the Viterbi algorithm.
* Given an output sequence or a set of such sequences, find the most likely set of state transition and output probabilities. In other words, discover the parameters of the HMM given a dataset of sequences. This problem is solved by the Baum-Welch algorithm.

A concrete example

"This example is further elaborated in the Viterbi algorithm page."

Applications of hidden Markov models

* Cryptanalysis
* Speech recognition
* Machine translation
* Partial discharge

History

Hidden Markov Models were first described in a series of statistical papers by Leonard E. Baum and other authors in the second half of the 1960s. One of the first applications of HMMs was speech recognition, starting in the mid-1970s. [Rabiner, p. 258]

In the second half of the 1980s, HMMs began to be applied to the analysis of biological sequences, in particular DNA. Since then, they have become ubiquitous in the field of bioinformatics. [Durbin et al.]

ee also

* Bayesian inference
* Estimation theory
* Hierarchical hidden Markov model
* Layered hidden Markov model
* Hidden semi-Markov model
* Variable-order Markov model
* Sequential dynamical system
* Conditional random field

Notes

References

* Lawrence R. Rabiner, "A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition," "Proceedings of the IEEE", 77 (2), p. 257–286, February 1989. [http://www.ece.ucsb.edu/Faculty/Rabiner/ece259/Reprints/tutorial%20on%20hmm%20and%20applications.pdf] [http://www.cs.cornell.edu/courses/cs481/2004fa/rabiner.pdf]
* Cite book
author = Richard Durbin, Sean R. Eddy, Anders Krogh, Graeme Mitchison
title = Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids
publisher = Cambridge University Press
year = 1999
isbn = 0-521-62971-3
* Lior Pachter and Bernd Sturmfels. "Algebraic Statistics for Computational Biology". Cambridge University Press, 2005. ISBN 0-521-85700-7.
* Olivier Cappé, Eric Moulines, Tobias Rydén. "Inference in Hidden Markov Models", Springer, 2005. ISBN 0-387-40264-0.
* Kristie Seymore, Andrew McCallum, and Roni Rosenfeld. "Learning Hidden Markov Model Structure for Information Extraction". AAAI 99 Workshop on Machine Learning for Information Extraction, 1999 "(also at CiteSeer: [http://citeseer.ist.psu.edu/seymore99learning.html] )".
* Tutorial from University of Leeds [http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html] .
* [http://www.stat.psu.edu/~jiali J. Li] , A. Najmi, R. M. Gray, Image classification by a two dimensional hidden Markov model, "IEEE Transactions on Signal Processing", 48(2):517-33, February 2000.
* Y. Ephraim and N. Merhav, Hidden Markov processes, IEEE Trans. Inform. Theory, vol. 48, pp. 1518-1569, June 2002.
* B. Pardo and W. Birmingham. [http://www.cs.northwestern.edu/~pardo/publications/pardo-birmingham-aaai-05.pdf Modeling Form for On-line Following of Musical Performances] . AAAI-05 Proc., July 2005.
* Thad Starner, Alex Pentland. [http://citeseer.ist.psu.edu/starner95visual.html Visual Recognition of American Sign Language Using Hidden Markov] . Master's Thesis, MIT, Feb 1995, Program in Media Arts
* L.Satish and B.I.Gururaj. [http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=212242 Use of hidden Markov models for partial discharge pattern classification] .IEEE Transactions on Dielectrics and Electrical Insulation, Apr 1993.The path-counting algorithm, an alternative to the Baum-Welch algorithm:
* [http://citeseer.ist.psu.edu/677948.html Comparing and Evaluating HMM Ensemble Training Algorithms Using Train and Test and Condition Number Criteria] , Journal of Pattern Analysis and Applications, 2003.

External links

* [http://www.cs.ubc.ca/~murphyk/Software/HMM/hmm.html Hidden Markov Model (HMM) Toolbox for Matlab] "(by Kevin Murphy)"
* [http://htk.eng.cam.ac.uk/ Hidden Markov Model Toolkit (HTK)] "(a portable toolkit for building and manipulating hidden Markov models)"
* [http://www.cs.brown.edu/research/ai/dynamics/tutorial/Documents/HiddenMarkovModels.html Hidden Markov Models] "(an exposition using basic mathematics)"
* [http://www.ghmm.org GHMM Library] "(home page of the GHMM Library project)"
* [http://www.run.montefiore.ulg.ac.be/~francois/software/jahmm/ Jahmm Java Library] "(Java library and associated graphical application)"
* [http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html A step-by-step tutorial on HMMs] "(University of Leeds)"
* [http://www.treeage.com/products/overviewHealth.html Software for Markov Models and Processes] " (TreeAge Software)"
* [http://jedlik.phy.bme.hu/~gerjanos/HMM/node2.html Hidden Markov Models] "(by Narada Warakagoda)"
* [http://www.kanungo.com/software/software.html HMM and other statistical programs] "(Implementation in C by Tapas Kanungo)"
* [http://hackage.haskell.org/cgi-bin/hackage-scripts/package/hmm The hmm package] A [http://www.haskell.org Haskell] library for working with Hidden Markov Models.
* [http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/forward_algorithm/s1_pg7.html Forward algorithm]