Powerset construction

In the theory of computation and Automata theory, the powerset construction or subset construction is a standard method for converting a nondeterministic finite automaton (NFA) into a deterministic finite automaton (DFA) which recognizes the same formal language. It is important in theory because it establishes that NFAs, despite their additional flexibility, are unable to recognize any language that cannot be recognized by some DFA. It is also important in practice for converting easier-to-construct NFAs into more efficiently executable DFAs. However, if the NFA has n states, the resulting DFA may have up to 2ⁿ states, an exponentially larger number, which sometimes makes the construction impractical for large NFAs.

The construction, sometimes called the Rabin–Scott powerset construction (or subset construction) to distinguish it from similar constructions for other types of automata, was first published by M. O. Rabin and Dana Scott in 1959.

Intuition

To simulate the operation of a DFA on a given input string, one needs to keep track of a single state at any time: the state that the automaton will reach after seeing a prefix of the input. However, to simulate an NFA, one needs to keep track of a set of states: all of the states that the automaton could reach after seeing the same prefix of the input, according to the nondeterministic choices made by the automaton. If, after a certain prefix of the input, a set S of states can be reached, then after the next input symbol x the set of reachable states is a deterministic function of S and x. Therefore, the sets of reachable NFA states play the same role in the NFA simulation as single DFA states play in the DFA simulation, and in fact the sets of NFA states appearing in this simulation may be re-interpreted as being states of a DFA.

Construction

The powerset construction applies most directly to an NFA that does not allow state transformations without consuming input symbols (aka: "ε-moves"). Such an automaton may be defined as a 5-tuple (Q, Σ, T, q₀, F), in which Q is the set of states, Σ is the set of input symbols, T is the transition function (mapping a state and an input symbol to a set of states), q₀ is the initial state, and F is the set of accepting states. The corresponding DFA has states corresponding to subsets of Q. The initial state of the DFA is {q₀}, the (one-element) set of initial states. The transition function of the DFA maps a state S (representing a subset of Q) and an input symbol x to the set T(S,x) = ∪{T(q,x) | q ∈ Q}, the set of all states that can be reached by an x-transition from a state in S. A state S of the DFA is an accepting state if and only if at least one member of S is an accepting state of the NFA.

In the simplest version of the powerset construction, the set of all states of the DFA is the powerset of Q, the set of all possible subsets of Q. However, many states of the resulting DFA may be useless as they may be unreachable from the initial state. An alternative version of the construction creates only the states that are actually reachable. For an NFA with ε-moves, the construction must be modified somewhat. In this case, the initial state consists of all NFA states reachable by ε-moves from q₀, and the value T(S,x) of the transition function is the set of all states reachable by ε-moves from ∪{T(q,x) | q in Q}.

It is also possible for the NFA to have more than one initial state. In this case, the initial state of the corresponding DFA is the set of all initial states of the NFA, or (if the NFA also has ε-moves) the set of all states reachable from initial states by ε-moves.

Example

The NFA below has four states; state 1 is initial, and states 3 and 4 are accepting. Its alphabet consists of the two symbols 0 and 1, and it has ε-moves. Its initial state is state 1.

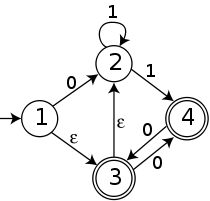
The initial state of the DFA constructed from this NFA is the set of all NFA states that are reachable from state 1 by ε-moves; that is, it is the set {1,2,3}. A transition from {1,2,3} by input symbol 0 must follow either the arrow from state 1 to state 2, or the arrow from state 3 to state 4. Additionally, neither state 2 nor state 4 have outgoing ε-moves. Therefore, T({1,2,3},0) = {2,4}, and by the same reasoning the full DFA constructed from the NFA is as shown below.

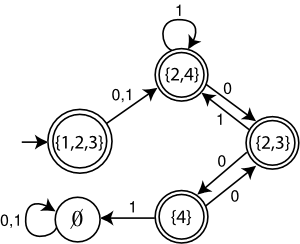
As can be seen in this example, there are five states reachable from the start state of the DFA; the remaining 11 sets in the powerset of the set of NFA states are not reachable.

Complexity

Because the DFA states consist of sets of NFA states, an n-state NFA may be converted to a DFA with at most 2ⁿ states. For every n, there exist n-state NFAs such that every subset of states is reachable from the initial subset, so that the converted DFA has exactly 2ⁿ states. A simple example requiring nearly this many states is the language of strings over the alphabet {0,1} in which there are at least n characters, the nth from last of which is 1. It can be represented by an (n + 1)-state NFA, but it requires 2ⁿ DFA states, one for each n-character suffix of the input.

Applications

Brzozowski's algorithm for DFA minimization uses the powerset construction, twice. It converts the input DFA into an NFA for the reverse language, by reversing all its arrows and exchanging the roles of initial and accepting states, converts the NFA back into a DFA using the powerset construction, and then repeats its process. Its worst-case complexity is exponential, unlike some other known DFA minimization algorithms, but in many examples it performs more quickly than its worst-case complexity would suggest.

Safra's construction, which converts a non-deterministic Büchi automaton with n states into a deterministic Muller automaton or into a deterministic Rabin automaton with 2^{O(n log n)} states, uses the powerset construction as part of its machinery.

References

• Michael Sipser, Introduction to the Theory of Computation ISBN 0-534-94728-X. (See . Theorem 1.19, section 1.2, pg. 55.)
• John E. Hopcroft and Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley Publishing, Reading Massachusetts, 1979. ISBN 0-201-02988-X. (See chapter 2.)
• James Andrew Anderson; Thomas J. Head (2006). Automata theory with modern applications. Cambridge University Press. pp. 43–49. ISBN 9780521848879. http://books.google.com/books?id=ikS8BLdLDxIC&pg=PA43. 
• Klaus Schneider (2004). Verification of reactive systems: formal methods and algorithms. Springer. pp. 210–212. ISBN 9783540002963. http://books.google.com/books?id=Z92bL1VrD_sC&pg=PA210. 
• M. O. Rabin and D. Scott. Finite automata and their decision problems. IBM Journal of Research and Development, 3(2):114–125, 1959