Rectangle method

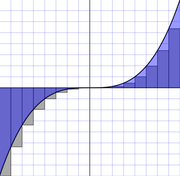
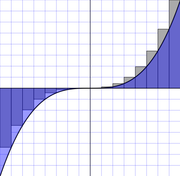
In mathematics, specifically in integral calculus, the rectangle method (also called the midpoint or mid-ordinate rule) computes an approximation to a definite integral, made by finding the area of a collection of rectangles whose heights are determined by the values of the function.

Specifically, the interval (a,b) over which the function is to be integrated is divided into N equal subintervals of length h = (b − a) / N. The rectangles are then drawn so that either their left or right corners, or the middle of their top line lies on the graph of the function, with bases running along the x-axis. The approximation to the integral is then calculated by adding up the areas (base multiplied by height) of the N rectangles, giving the formula:

$\int_a^b f(x)\,dx \approx h \sum_{n=0}^{N-1} f(x_{n})$

where h = (b − a) / N and x_n = a + nh.

The formula for x_n above gives x_n for the Top-left corner approximation.

As N gets larger, this approximation gets more accurate. In fact, this computation is the spirit of the definition of the Riemann integral and the limit of this approximation as $n \to \infty$ is defined and equal to the integral of f on (a,b) if this Riemann integral is defined. Note that this is true regardless of which i' is used, however the midpoint approximation tends to be more accurate for finite n.

The different rectangle approximations

Top-left corner approximation   Midpoint approximation   Top-right corner approximation

Error

For a function f which is twice differentiable, the approximation error in each section (a,a + Δ) of the midpoint rule decays as the cube of the width of the rectangle. (For a derivation based on a Taylor approximation, see Midpoint method)

$E_i \le \frac{\Delta^3}{24}\,f''(\xi)$

for some ξ in (a,a + Δ). Summing this, the approximation error for n intervals with width Δ is less than or equal to

n = 1,2,3,...

where n + 1 is the number of nodes

$E \le \frac{n\Delta^3}{24}f''(\xi)$

in terms of the total interval, we know that nΔ = b − a so we can rewrite the expression:

$E \le \frac{(b-a)\Delta^2}{24}f''(\xi)$

for some ξ in (a,b).

Matlab Example Program

 
function [F] = rectangle( a, b, n )
 
%*******************************************************
 
% This function computes an approximation to a definite
% integral using rectangle method. Input variables are
% a=initial value, b=end value, n=number of iterations.
% Author: User:Gulmammad
% Modified: User:fOx
% Modified: User:cholericfun
 
%*******************************************************
 
h = ( b - a ) / n ;
 
F = 0 ;
 
 
% x = [0 , h*[1 : n-1]];          % for the left corner:  O(h)
  x = [a+.5*h,a+.5*h+h*[1:n-1]];      % for the center:       O(h²)
% x = [1:n]*h;                    % for the right corner: O(h)
 
for i = 1 : n
 
    F = F + f( x(i) ) * h ;
 
end
 
 
function [func] = f( x )
 
        func = 3 * x.^2 ; %specify your function here
 
    end
 
 
end

C example program

#include <stdio.h>
#include <math.h>
 
double f(double x){
   return sin(x);
}
 
double rectangle_integrate(double a, double b, int subintervals, double (*function)(double) ){
   double result;
   double interval;
   int i;
 
   interval=(b-a)/subintervals;
   result=0;
 
   for(i=1;i<=subintervals;i++){
      result+=function(a+interval*(i-0.5));
   }
   result*=interval;
 
   return result;
}
 
int main(void){
   double integral;
   integral=rectangle_integrate(0,2,100,f);
   printf("The value of the integral is: %f \n",integral);
   return 0;
}

Fortran Example Program

PROGRAM Calc
   IMPLICIT NONE
   DOUBLE PRECISION y, a, b, dx, xi
   INTEGER n, i
   DATA y /0.0d0/
 
   PRINT*, 'Enter the start, end and numer of intervals:'
   READ*, a, b, n
 
   dx = (b-a)/n
 
   DO i = 1, n
      xi = a + (i-0.5d0)*dx
      y = y + f(xi)*dx
   END DO
 
   PRINT*, 'Quadrature of f(x):', y
 
CONTAINS
 
   FUNCTION f(x)
      DOUBLE PRECISION f, x
      f = 4.0d0/(1.0d0 + x**2)
   END FUNCTION F
 
END PROGRAM Calc

See also

• Midpoint method for solving ordinary differential equations
• Trapezoidal rule
• Simpson's rule