Simpson's rule

Simpson's rule can be derived by approximating the integrand f (x) (in blue) by the quadratic interpolant P (x) (in red).

In numerical analysis, Simpson's rule is a method for numerical integration, the numerical approximation of definite integrals. Specifically, it is the following approximation:

$\int_{a}^{b} f(x) \, dx \approx \frac{b-a}{6}\left[f(a) + 4f\left(\frac{a+b}{2}\right)+f(b)\right].$

Simpson's rule also corresponds to the 3-point Newton-Cotes quadrature rule.

The method is credited to the mathematician Thomas Simpson (1710–1761) of Leicestershire, England. Kepler used similar formulas over 100 years prior and in German the method is sometimes called Keplersche Fassregel for this reason.

Simpson's rule is a staple of scientific data analysis and engineering. It is widely used, for example, by Naval architects to calculate the capacity of a ship or lifeboat.^[1]

Derivation

Simpson's rule can be derived in various ways.

Quadratic interpolation

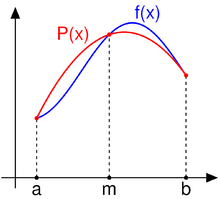
One derivation replaces the integrand f(x) by the quadratic polynomial P(x) which takes the same values as f(x) at the end points a and b and the midpoint m = (a + b) / 2. One can use Lagrange polynomial interpolation to find an expression for this polynomial,

$P(x) = f(a) \frac{(x-m)(x-b)}{(a-m)(a-b)} + f(m) \frac{(x-a)(x-b)}{(m-a)(m-b)} + f(b) \frac{(x-a)(x-m)}{(b-a)(b-m)}.$

An easy (albeit tedious) calculation shows that

$\int_{a}^{b} P(x) \, dx =\frac{b-a}{6}\left[f(a) + 4f\left(\frac{a+b}{2}\right)+f(b)\right].$ ^[2]

This calculation can be carried out more easily if one first observes that (by scaling) there is no loss of generality in assuming that a = − 1 and b = 1.

Averaging the midpoint and the trapezoidal rules

Another derivation constructs Simpson's rule from two simpler approximations: the midpoint rule

$M = (b-a) f \left( \frac{a+b}{2} \right)$

and the trapezoidal rule

$T = \tfrac12 (b-a) (f(a)+f(b)).$

The errors in these approximations are

$-\tfrac1{ 24} (b-a)^3 f''(a) + O((b-a)^4) \quad\text{and}\quad \tfrac1{12} (b-a)^3 f''(a) + O((b-a)^4),$

respectively. It follows that the leading error term vanishes if we take the weighted average

$\frac{2M+T}{3}.$

This weighted average is exactly Simpson's rule.

Using another approximation (for example, the trapezoidal rule with twice as many points), it is possible to take a suitable weighted average and eliminate another error term. This is Romberg's method.

Undetermined coefficients

The third derivation starts from the ansatz

$\frac{1}{b-a} \int_{a}^{b} f(x) \, dx \approx \alpha f(a) + \beta f\left(\frac{a+b}{2}\right) + \gamma f(b).$

The coefficients α, β and γ can be fixed by requiring that this approximation be exact for all quadratic polynomials. This yields Simpson's rule.

Error

The error in approximating an integral by Simpson's rule is

$\frac{1}{90} \left(\frac{b-a}{2}\right)^5 \left|f^{(4)}(\xi)\right|,$

where ξ is some number between a and b.^[3]

The error is asymptotically proportional to (b − a)⁵. However, the above derivations suggest an error proportional to (b − a)⁴. Simpson's rule gains an extra order because the points at which the integrand is evaluated are distributed symmetrically in the interval [a, b].

Simpson's rule provides exact results for any polynomial of degree three or less, since the error term involves the fourth derivative of f.

Composite Simpson's rule

If the interval of integration [a,b] is in some sense "small", then Simpson's rule will provide an adequate approximation to the exact integral. By small, what we really mean is that the function being integrated is relatively smooth over the interval [a,b]. For such a function, a smooth quadratic interpolant like the one used in Simpson's rule will give good results.

However, it is often the case that the function we are trying to integrate is not smooth over the interval. Typically, this means that either the function is highly oscillatory, or it lacks derivatives at certain points. In these cases, Simpson's rule may give very poor results. One common way of handling this problem is by breaking up the interval [a,b] into a number of small subintervals. Simpson's rule is then applied to each subinterval, with the results being summed to produce an approximation for the integral over the entire interval. This sort of approach is termed the composite Simpson's rule.

Suppose that the interval [a,b] is split up in n subintervals, with n an even number. Then, the composite Simpson's rule is given by

$\int_a^b f(x) \, dx\approx \frac{h}{3}\bigg[f(x_0)+2\sum_{j=1}^{n/2-1}f(x_{2j})+ 4\sum_{j=1}^{n/2}f(x_{2j-1})+f(x_n) \bigg],$

where x_j = a + jh for j = 0,1,...,n − 1,n with h = (b − a) / n; in particular, x₀ = a and x_n = b. The above formula can also be written as

$\int_a^b f(x) \, dx\approx \frac{h}{3}\bigg[f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+2f(x_4)+\cdots+4f(x_{n-1})+f(x_n)\bigg].$

The error committed by the composite Simpson's rule is bounded (in absolute value) by

$\frac{h^4}{180}(b-a) \max_{\xi\in[a,b]} |f^{(4)}(\xi)|,$

where h is the "step length", given by h = (b − a) / n.^[4]

This formulation splits the interval [a,b] in subintervals of equal length. In practice, it is often advantageous to use subintervals of different lengths, and concentrate the efforts on the places where the integrand is less well-behaved. This leads to the adaptive Simpson's method.

Alternative extended Simpson's rule

This is another formulation of a composite Simpson's rule: instead of applying Simpson's rule to disjoint segments of the integral to be approximated, Simpson's rule is applied to overlapping segments, yielding:^[5]

$\int_a^b f(x) \, dx\approx \frac{h}{48}\bigg[17f(x_0)+59f(x_1)+43f(x_2)+49f(x_3)+48 \sum_{i=4}^{n-4} f(x_i)+49f(x_{n-3})+43f(x_{n-2})+59f(x_{n-1})+17f(x_n)\bigg].$

Simpson's 3/8 rule

Simpson's 3/8 rule is another method for numerical integration proposed by Thomas Simpson. It is based upon a cubic interpolation rather than a quadratic interpolation. Simpson's 3/8 rule is as follows:

$\int_{a}^{b} f(x) \, dx \approx \frac{3h}{8}\left[f(a) + 3f\left(\frac{2a+b}{3}\right) + 3f\left(\frac{a+2b}{3}\right) + f(b)\right] = \frac{(b-a)}{8}\left[f(a) + 3f\left(\frac{2a+b}{3}\right) + 3f\left(\frac{a+2b}{3}\right) + f(b)\right].$

The error of this method is:

$\left|\frac{(b-a)^5}{6480} f^{(4)}(\xi)\right|,$

where ξ is some number between a and b. Thus, the 3/8 rule is about twice as accurate as the standard method, but it uses one more function value. A composite 3/8 rule also exists, similarly as above.^[6]

Simpson's 3/8 rule is used by Naval architects to calculate a merchant cargo ship's lifeboat capacity.

Sample implementation

An implementation of the composite Simpson's rule in pylab:

def simpson(f, a, b, n):
    """f=function, a=initial value, b=end value, n=number of double intervals of size 2h"""
 
    n *= 2
    h = (b - a) / n;
    S = f(a)
 
    for i in range(1, n, 2):
        x = a + h * i
        S += 4 * f(x)
 
    for i in range(2, n-1, 2):
        x = a + h * i
        S += 2 * f(x)
 
    S += f(b)
    F = h * S / 3
 
    return F

See also

• Gaussian quadrature
• Rectangle method
• Trapezoidal rule

Notes

1. ^ McCall Pate (1918). The naval artificer's manual: (The naval artificer's handbook revised) text, questions and general information for deck. United States. Bureau of Reconstruction and Repair. p. 198. http://books.google.com/books?id=bQc9AAAAYAAJ&pg=PA198. 
2. ^ Atkinson, p. 256; Süli and Mayers, §7.2
3. ^ Atkinson, equation (5.1.15); Süli and Mayers, Theorem 7.2
4. ^ Atkinson, pp. 257+258; Süli and Mayers, §7.5
5. ^ Press (1989), p. 122
6. ^ Matthews (2004)

References

• Atkinson, Kendall E. (1989). An Introduction to Numerical Analysis (2nd ed.). John Wiley & Sons. ISBN 0-471-50023-2. 
• Burden, Richard L. and Faires, J. Douglas (2000). Numerical Analysis (7th ed.). Brooks/Cole. ISBN 0-534-38216-9. 
• Matthews, John H. (2004). "Simpson's 3/8 Rule for Numerical Integration". Numerical Analysis - Numerical Methods Project. California State University, Fullerton. http://math.fullerton.edu/mathews/n2003/Simpson38RuleMod.html. Retrieved 11 November 2008. 
• Press, William H., Brian P. Flannery, William T. Vetterling, and Saul A. Teukolsky (1989). Numerical Recipes in Pascal: The Art of Scientific Computing. Cambridge University Press. ISBN 0521375169. http://books.google.com/?id=bh5w6E-M-PUC&pg=PA122&dq=extended-simpson%27s-rule. 
• Süli, Endre and Mayers, David (2003). An Introduction to Numerical Analysis. Cambridge University Press. ISBN 0-521-81026-4 (hardback), ISBN 0-521-00794-1 (paperback). 
• Kaw, Autar; Kalu, Egwu (2008). "Numerical Methods with Applications". [1]. .
• Weisstein, Eric W. (2010). "Newton-Cotes Formulas". MathWorld--A Wolfram Web Resource.. MathWorld. http://mathworld.wolfram.com/Newton-CotesFormulas.html. Retrieved 2 August 2010. 

External links

• Weisstein, Eric W., "Simpson's Rule" from MathWorld.
• Simpson's Rule for Numerical Integration
• Application of Simpson's Rule - Earthwork Excavation (Note: The formula described in this page is correct but there are errors in the calculation which should give a result of 569m3 and not 623m3 as stated)
• Simpson's 1/3rd rule of integration - Notes, PPT, Mathcad, Matlab, Mathematica, Maple at Numerical Methods for STEM undergraduate
• A detailed description of a computer implementation is described by Dorai Sitaram in Teach Yourself Scheme in Fixnum Days, Appendix C
• C Language Program to Implement Simpson's Rule

This article incorporates material from Code for Simpson's rule on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.