- P-rep
-
In statistical hypothesis testing, p-rep or prep has been proposed as a statistical alternative to the classic p-value. [1] Whereas a p-value is the probability of obtaining a result under the null hypothesis, p-rep computes the probability of replicating an effect. Whether it does so is heavily disputed – some have argued that the concept rests on a mathematical falsehood.
For a while, the Association for Psychological Science recommended that articles submitted to Psychological Science and their other journals report p-rep rather than the classic p-value,[2] but this is no longer the case.[3]
Contents
Calculation
The value of the p-rep (prep) can be approximated based on the p-value (p) as follows:
Criticism
The fact that the p-rep has a one-to-one correspondence with the p-value makes it clear that this new measure doesn't bring any additional information on the significance of the result of a given experiment. However, according to Killeen who acknowledges this latter point, the main advantage of p-rep lies in the fact that it better captures the way experimenters naively think and conceptualize p-values and statistical hypothesis testing.
Among the criticisms of p-rep is the fact that it does not take prior probabilities into account.[4] For example, if an experiment on some unlikely paranormal phenomenon produced a p-rep of 0.75, most right-thinking people would not believe the probability of a replication is 0.75. Instead they would conclude that it is much closer to 0. Extraordinary claims require extraordinary evidence, and p-rep ignores this. This consideration undermines the argument that p-rep is easier to understand than a classical p value. The fact that p-rep requires assumptions about prior probabilities for it to be valid makes its interpretation complex. The classical p merely states the probability of an outcome (or more extreme outcome) given a null hypothesis and therefore is valid without regard to prior probabilities. Killeen argues that new results should be evaluated in their own right, without the burden of history, with flat priors: that is what p-rep yields. A more pragmatic estimate of replicability would include prior knowledge, which the logic of p-rep permits, but which null testing does not.
Critics have also underscored mathematical errors in the original paper by Killeen. For example, the formula relating the effect sizes from two replications of a given experiment erroneously uses one of these random variables as a parameter of the probability distribution of the other while he previously hypothesized these two variables to be independent.[5][unreliable source] These criticisms were addressed in his rejoinder.[6]
A further criticism of the P-rep statistic involves the logic of experimentation. The purpose of replication in science is to adequately account for unmeasured factors in the testing environment, and in the case of human-subjects research: unmeasured participant variables and response biases, characteristics of the individual(s) conducting the experiment, and to replicate findings using different samples of participants. The idea that any value can, from one sample of data, meaningfully capture the likelihood of (by definition) unmeasured factors to affect the outcome, and thus the likelihhod of replicability, is a logical fallacy.[citation needed]
References
- ^ Killeen PR (2005). "An alternative to null-hypothesis significance tests". Psychological science : a journal of the American Psychological Society / APS 16 (5): 345–53. doi:10.1111/j.0956-7976.2005.01538.x. PMC 1473027. PMID 15869691. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=1473027.
- ^ archived version of "Psychological Science Journal, Author Guidelines"
- ^ Psychological Science Journal, Author Guidelines.
- ^ Macdonald, R. R. (2005) "Why Replication Probabilities Depend on Prior Probability Distributions" Psychological Science, 2005, 16, 1006–1008 [1]
- ^ "p-rep" at Pro Bono Statistics
- ^ Killeen, P. R. (2005)" Replicability, Confidence, and Priors", Psychological Science, 2005, 16, 1009–1012 [2]
External links
Categories:- Statistical tests
- Hypothesis testing
Wikimedia Foundation. 2010.

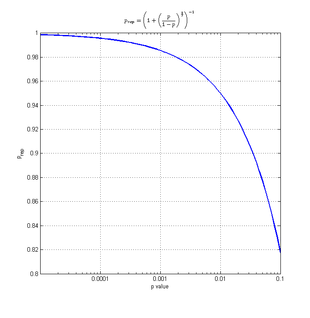
![p_\text{rep} = \left[ 1 + \left( \frac{p}{1-p} \right)^{\frac{2}{3}} \right]^{-1}.](c/ffc8b52bac9bd21761e40723a5f846c4.png)