Chebyshev rational functions

This article is not about the Chebyshev rational functions used in the design of elliptic filters. For those functions, see Elliptic rational functions.

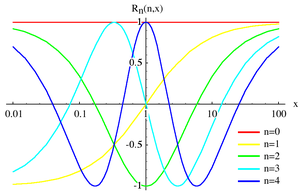
Plot of the Chebyshev rational functions for n=0,1,2,3 and 4 for x between 0.01 and 100.

In mathematics, the Chebyshev rational functions are a sequence of functions which are both rational and orthogonal. They are named after Pafnuty Chebyshev. A rational Chebyshev function of degree n is defined as:

$R_n(x)\ \stackrel{\mathrm{def}}{=}\ T_n\left(\frac{x-1}{x+1}\right)$

where T_n(x) is a Chebyshev polynomial of the first kind.

Properties

Many properties can be derived from the properties of the Chebyshev polynomials of the first kind. Other properties are unique to the functions themselves.

Recursion

$R_{n+1}(x)=2\,\frac{x-1}{x+1}R_n(x)-R_{n-1}(x)\quad\mathrm{for\,n\ge 1}$

Differential equations

$(x+1)^2R_n(x)=\frac{1}{n+1}\frac{d}{dx}\,R_{n+1}(x)-\frac{1}{n-1}\frac{d}{dx}\,R_{n-1}(x) \quad\mathrm{for\,n\ge 2}$

$(x+1)^2x\frac{d^2}{dx^2}\,R_n(x)+\frac{(3x+1)(x+1)}{2}\frac{d}{dx}\,R_n(x)+n^2R_{n}(x) = 0$

Orthogonality

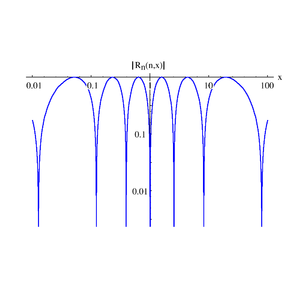
Plot of the absolute value of the seventh order (n=7) Chebyshev rational function for x between 0.01 and 100. Note that there are n zeroes arranged symmetrically about x=1 and if x₀ is a zero, then 1/x₀ is a zero as well. The maximum value between the zeros is unity. These properties hold for all orders.

Defining:

$\omega(x) \ \stackrel{\mathrm{def}}{=}\ \frac{1}{(x+1)\sqrt{x}}$

The orthogonality of the Chebyshev rational functions may be written:

$\int_{0}^\infty R_m(x)\,R_n(x)\,\omega(x)\,dx=\frac{\pi c_n}{2}\delta_{nm}$

where c_n equals 2 for n=0 and c_n equals 1 for $n \ge 1$ and δ_nm is the Kronecker delta function.

Expansion of an arbitrary function

For an arbitrary function $f(x)\in L_\omega^2$ the orthogonality relationship can be used to expand f(x):

$f(x)=\sum_{n=0}^\infty F_n R_n(x)$

where

$F_n=\frac{2}{c_n\pi}\int_{0}^\infty f(x)R_n(x)\omega(x)\,dx.$

Particular values

$R_0(x)=1\,$

$R_1(x)=\frac{x-1}{x+1}\,$

$R_2(x)=\frac{x^2-6x+1}{(x+1)^2}\,$

$R_3(x)=\frac{x^3-15x^2+15x-1}{(x+1)^3}\,$

$R_4(x)=\frac{x^4-28x^3+70x^2-28x+1}{(x+1)^4}\,$

$R_n(x)=\frac{1}{(x+1)^n}\sum_{m=0}^{n} (-1)^m{2n \choose 2m}x^{n-m}\,$

Partial fraction expansion

$R_n(x)=\sum_{m=0}^{n} \frac{(m!)^2}{(2m)!}{n+m-1 \choose m}{n \choose m}\frac{(-4)^m}{(x+1)^m}$

References

• Ben-Yu, Guo; Jie, Shen; Zhong-Quing, Wang (2002). "Chebyshev rational spectral and pseudospectral methods on a semi-infinite interval" (PDF). Int. J. Numer. Meth. Engng 53: 65–84. doi:10.1002/nme.392. http://www.math.purdue.edu/~shen/pub/GSW_IJNME02.pdf. Retrieved 2006-07-25.