Composition (number theory)

For other uses, see Composition (disambiguation).

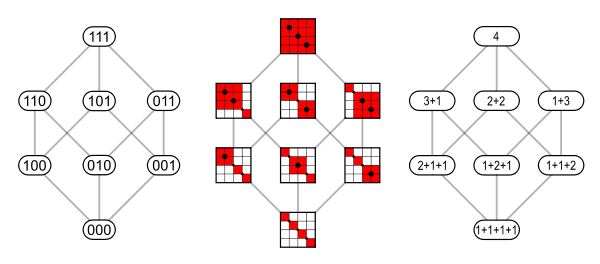
In mathematics, a composition of an integer n is a way of writing n as the sum of a sequence of (strictly) positive integers. Two sequences that differ in the order of their terms define different compositions of their sum, while they are considered to define the same partition of that number. Any integer has finitely many distinct compositions. Negative numbers do not have any compositions, but 0 has one composition, the empty sequence. Any positive integer n has 2ⁿ⁻¹ distinct compositions. This is a power of two, because every composition matches a binary number.

Bijection between 3 bit binary numbers and compositions of 4

A weak composition of an integer n is similar to a composition of n, but allowing terms of the sequence to be zero: it is a way of writing n as the sum of a sequence of non-negative integers. As a consequence any positive integer admits infinitely many weak compositions (if their length is not bounded). Adding a number of terms 0 to the end of a weak composition is usually not considered to define a different weak composition, in other words weak compositions are assumed to be implicitly extended indefinitely by terms 0.

Examples

The 32 compositions of 6

1 + 1 + 1 + 1 + 1 + 1
2 + 1 + 1 + 1 + 1
1 + 2 + 1 + 1 + 1
...
1 + 5
6

The 11 partitions of 6

1 + 1 + 1 + 1 + 1 + 1
2 + 1 + 1 + 1 + 1
3 + 1 + 1 + 1
...
3 + 3
6

The sixteen compositions of 5 are:

• 5
• 4+1
• 3+2
• 3+1+1
• 2+3
• 2+2+1
• 2+1+2
• 2+1+1+1
• 1+4
• 1+3+1
• 1+2+2
• 1+2+1+1
• 1+1+3
• 1+1+2+1
• 1+1+1+2
• 1+1+1+1+1.

Compare this with the seven partitions of 5:

• 5
• 4+1
• 3+2
• 3+1+1
• 2+2+1
• 2+1+1+1
• 1+1+1+1+1.

It is possible to put constraints on the parts of the compositions. For example the five compositions of 5 into distinct terms are:

• 5
• 4+1
• 3+2
• 2+3
• 1+4.

Compare this with the three partitions of 5 into distinct terms:

• 5
• 4+1
• 3+2.

Number of compositions

Conventionally the empty composition is counted as the sole composition of 0, and there are no compositions of negative integers. There are 2ⁿ⁻¹ compositions of n ≥ 1; here is a proof:

Placing either a plus sign or a comma in each of the n − 1 boxes of the array

$\big(\, \overbrace{1\, \square\, 1\, \square\, \ldots\, \square\, 1\, \square\, 1}^n\, \big)$

produces a unique composition of n. Conversely, every composition of n determines an assignment of pluses and commas. Since there are n − 1 binary choices, the result follows. The same argument shows that the number of compositions of n into exactly k parts is given by the binomial coefficient ${n-1\choose k-1}$. Note that by summing over all possible number of parts we recover 2ⁿ⁻¹ as the total number of compositions of n:

$\sum_{k=1}^{n} {n-1 \choose k-1} = 2^{n-1}.$

For weak compositions, the number is ${n+k-1\choose k-1}$, since each k-composition of n + k corresponds to a weak one of n by the rule [a + b + ... + c = n + k] → [(a − 1) + (b − 1) + ... + (c − 1) = n].

References

• "Combinatorics of Compositions and Words", Silvia Heubach, Toufik Mansour, CRC Press, 2009, ISBN 9781420072679.

External links

• Partition and composition calculator