- Lambert's cosine law
-
In optics, Lambert's cosine law says that the radiant intensity observed from a Lambertian surface or a Lambertian radiator is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal. A Lambertian surface is also known as an ideal diffusely reflecting surface. The law is also known as the cosine emission law or Lambert's emission law. It is named after Johann Heinrich Lambert, from his Photometria, published in 1760.
An important consequence of Lambert's cosine law is that when a Lambertian surface is viewed from any angle, it has the same radiance. This means, for example, that to the human eye it has the same apparent brightness (or luminance). It has the same radiance because, although the emitted power from a given area element is reduced by the cosine of the emission angle, the apparent size (solid angle) of the observed area, as seen by a viewer, is decreased by a corresponding amount. Therefore, its radiance (power per unit solid angle per unit projected source area) is the same.
Contents
Lambertian scatterers and radiators
When an area element is radiating as a result of being illuminated by an external source, the irradiance (energy or photons/time/area) landing on that area element will be proportional to the cosine of the angle between the illuminating source and the normal. A Lambertian scatterer will then scatter this light according to the same cosine law as a Lambertian emitter. This means that although the radiance of the surface depends on the angle from the normal to the illuminating source, it will not depend on the angle from the normal to the observer. For example, if the moon were a Lambertian scatterer, one would expect to see its scattered brightness appreciably diminish towards the terminator due to the increased angle at which sunlight hit the surface. The fact that it does not diminish illustrates that the moon is not a Lambertian scatterer, and in fact tends to scatter more light into the oblique angles than would a Lambertian scatterer.
The emission of a Lambertian radiator does not depend upon the amount of incident radiation, but rather from radiation originating in the emitting body itself. For example, if the sun were a Lambertian radiator, one would expect to see a constant brightness across the entire solar disc. The fact that the sun exhibits limb darkening in the visible region illustrates that it is not a Lambertian radiator. A black body is an example of a Lambertian radiator.
Details of equal brightness effect
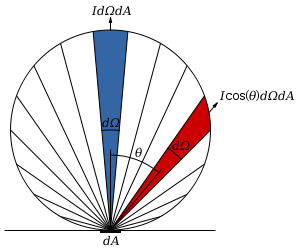
The situation for a Lambertian surface (emitting or scattering) is illustrated in Figures 1 and 2. For conceptual clarity we will think in terms of photons rather than energy or luminous energy. The wedges in the circle each represent an equal angle dΩ, and for a Lambertian surface, the number of photons per second emitted into each wedge is proportional to the area of the wedge.
It can be seen that the length of each wedge is the product of the diameter of the circle and cos(θ). It can also be seen that the maximum rate of photon emission per unit solid angle is along the normal and diminishes to zero for θ = 90°. In mathematical terms, the radiance along the normal is I photons/(s·cm2·sr) and the number of photons per second emitted into the vertical wedge is I dΩ dA. The number of photons per second emitted into the wedge at angle θ is I cos(θ) dΩ dA.
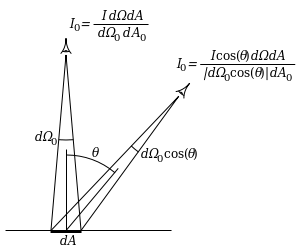
Figure 2 represents what an observer sees. The observer directly above the area element will be seeing the scene through an aperture of area dA0 and the area element dA will subtend a (solid) angle of dΩ0. We can assume without loss of generality that the aperture happens to subtend solid angle dΩ when "viewed" from the emitting area element. This normal observer will then be recording I dΩ dA photons per second and so will be measuring a radiance of
 photons/(s·cm2·sr).
photons/(s·cm2·sr).
The observer at angle θ to the normal will be seeing the scene through the same aperture of area dA0 and the area element dA will subtend a (solid) angle of dΩ0 cos(θ). This observer will be recording I cos(θ) dΩ dA photons per second, and so will be measuring a radiance of
 photons/(s·cm2·sr),
photons/(s·cm2·sr),
which is the same as the normal observer.
Relating peak luminous intensity and luminous flux
In general, the luminous intensity of a point on a surface varies by direction; for a Lambertian surface, that distribution is defined by the cosine law, with peak luminous intensity in the normal direction. Thus when the Lambertian assumption holds, we can calculate the total luminous flux, Ftot, from the peak luminous intensity, Imax, by integrating the cosine law:
and so
where sin(θ) is the determinant of the Jacobian matrix for the unit sphere, and realizing that Imax is luminous flux per steradian.[1] Similarly, the peak intensity will be
 of the total radiated luminous flux. For Lambertian surfaces, the same factor of
of the total radiated luminous flux. For Lambertian surfaces, the same factor of  relates luminance to luminous emittance, radiant intensity to radiant flux, and radiance to radiant emittance. Radians and steradians are, of course, dimensionless and so "rad" and "sr" are included only for clarity.
relates luminance to luminous emittance, radiant intensity to radiant flux, and radiance to radiant emittance. Radians and steradians are, of course, dimensionless and so "rad" and "sr" are included only for clarity.Example: A surface with a luminance of say 100 cd/m2 (= 100 nits, typical PC-screen) seen from the front, will (if it is a perfect Lambert emitter) emit a total luminous flux of 314 lm/m2. If it's a 19" screen (area ≈ 0.1 m2), the total light emitted would thus be 31.4 lm.
Uses
Lambert's cosine law in its reversed form (Lambertian reflection) implies that the apparent brightness of a Lambertian surface is proportional to cosine of the angle between the surface normal and the direction of the incident light.
This phenomenon is among others used when creating moldings, which are a means of applying light and dark shaded stripes to a structure or object without having to change the material or apply pigment. The contrast of dark and light areas gives definition to the object. Moldings are strips of material with various cross sections used to cover transitions between surfaces or for decoration.
See also
References
- ^ Incropera and DeWitt, Fundamentals of Heat and Mass Transfer, 5th ed., p.710.
Categories:
Wikimedia Foundation. 2010.