Uniform norm

This article is about the function space norm. For the finite-dimensional vector space distance, see Chebyshev distance.

The black square is the set of points in R² where the sup norm equals a fixed non-zero constant.

In mathematical analysis, the uniform norm assigns to real- or complex-valued bounded functions f defined on a set S the nonnegative number

$\|f\|_\infty=\|f\|_{\infty,S}=\sup\left\{\,\left|f(x)\right|:x\in S\,\right\}.$

This norm is also called the supremum norm, the Chebyshev norm, or the infinity norm.

If we allow unbounded functions, this formula does not yield a norm or metric in a strict sense, although the obtained so-called extended metric still allows one to define a topology on the function space in question.

If f is a continuous function on a closed interval, or more generally a compact set, then it is bounded and the supremum in the above definition is attained by the Weierstrass extreme value theorem, so we can replace the supremum by the maximum. In this case, the norm is also called the maximum norm.

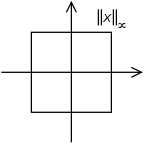
In particular, for the case of a vector $x=(x_1,\dots,x_n)$ in finite dimensional coordinate space, it takes the form

$\|x\|_\infty=\max\{ |x_1|, \dots, |x_n| \}.$

The reason for the subscript "∞" is that whenever f is continuous

$\lim_{p\rightarrow\infty}\|f\|_p=\|f\|_\infty,$

where

$\|f\|_p=\left(\int_D \left|f\right|^p\,d\mu\right)^{1/p}$

where D is the domain of f (and the integral amounts to a sum if D is a discrete set).

The binary function

$d(f,g)=\|f-g\|_\infty$

is then a metric on the space of all bounded functions (and, obviously, any of its subsets) on a particular domain. A sequence { f_n : n = 1, 2, 3, ... } converges uniformly to a function f if and only if

$\lim_{n\rightarrow\infty}\|f_n-f\|_\infty=0.\,$

For complex continuous functions over a compact space, this turns it into a C* algebra.

See also

• Chebyshev distance
• Uniform continuity
• Uniform convergence
• Uniform space