Hadwiger–Nelson problem

Unsolved problems in mathematics

How many colors are needed to color the plane so that no two points at unit distance are the same color?

In geometric graph theory, the Hadwiger–Nelson problem, named after Hugo Hadwiger and Edward Nelson, asks for the minimum number of colors required to color the plane such that no two points at distance one from each other have the same color. The answer is unknown, but has been narrowed down to one of the numbers 4, 5, 6 or 7. The correct value may actually depend on the choice of axioms for set theory (Shelah & Soifer 2003).

The question can be phrased in graph theoretic terms as follows. Let G be the unit distance graph of the plane: an infinite graph with all points of the plane as vertices and with an edge between two vertices if and only if there is unit distance between the two points. Then the Hadwiger–Nelson problem is to find the chromatic number of G. As a consequence, the problem is often called "finding the chromatic number of the plane". By the de Bruijn–Erdős theorem, a result of de Bruijn & Erdős (1951), the problem is equivalent (under the assumption of the axiom of choice) to that of finding the largest possible chromatic number of a finite unit distance graph.

According to Jensen & Toft (1995), the problem was first formulated by E. Nelson in 1950, and first published by Gardner (1960). Hadwiger (1945) published a related result, showing that any cover of the plane by five congruent closed sets contains a unit distance in one of the sets, and he also mentioned the problem in a later paper (Hadwiger 1961). Soifer (2008) discusses the problem and its history extensively.

Lower and upper bounds

A seven-coloring of the plane, and a four-chromatic unit distance graph in the plane, providing upper and lower bounds for the Hadwiger–Nelson problem.

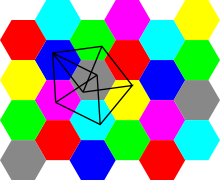
The fact that the chromatic number of the plane must be at least four follows from the existence of a seven-vertex unit distance graph, named the Moser spindle after its discovery by the brothers William and Leo Moser, with chromatic number four. This graph consists of two unit equilateral triangles joined at a common vertex–x. Each of these triangles is joined along another edge to another equilateral triangle; the vertices y and z of these joined triangles are at unit distance from each other. The Moser spindle may also be constructed graph-theoretically using the Hajós construction starting with two complete graphs on four vertices. If the plane could be three-colored, the coloring within the triangles would force y and z to both have the same color as x, but then, since y and z are at unit distance from each other, we would not have a proper coloring of the unit distance graph of the plane. Therefore, at least four colors are needed to color this graph and the plane containing it.

The upper bound of seven on the chromatic number follows from the existence of a tessellation of the plane by regular hexagons, with diameter slightly less than one, that can be assigned seven colors in a repeating pattern to form a 7-coloring of the plane; according to Soifer (2008), this upper bound was first observed by John R. Isbell.

Variations of the problem

The problem can easily be extended to higher dimensions. In particular, finding the chromatic number of space usually refers to the 3-dimensional version. As with the version on the plane, the answer is not known, but has been shown to be at least 6 and at most 15 (Coulson 2002; Radoičić and Tóth).

One can also consider colorings of the plane in which the sets of points of each color are restricted to sets of some particular type (see, e.g., Croft, Falconer & Guy 1991). Such restrictions may cause the required number of colors to increase, as they prevent certain colorings from being considered acceptable. For instance, if all color classes are required to be Lebesgue measurable, it is known that at least five colors are required. If all connected components of each color class are convex polygons with area bounded away from zero, then at least six colors are required (Coulson 2004).

See also

• Four color theorem

References

• de Bruijn, N. G.; Erdős, P. (1951), "A colour problem for infinite graphs and a problem in the theory of relations", Nederl. Akad. Wetensch. Proc. Ser. A 54: 371–373 .
• Chilakamarri, K. B. (1993), "The unit-distance graph problem: a brief survey and some new results", Bull Inst. Combin. Appl. 8: 39–60 .
• Coulson, D. (2004), "On the chromatic number of plane tilings", J. Austral. Math. Soc. 77 (2): 191–196, doi:10.1017/S1446788700013574, http://www.austms.org.au/Publ/JAustMS/V77P2/a83.html .
• Coulson, D. (2002), "A 15-colouring of 3-space omitting distance one", Discrete Math. 256: 83–90, doi:10.1016/S0012-365X(01)00183-2 .
• Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1991), Unsolved Problems in Geometry, Springer-Verlag , Problem G10.
• Gardner, Martin (1960), "Mathematical Games", Scientific American 203/4: 180 .
• Hadwiger, Hugo (1945), "Überdeckung des euklidischen Raumes durch kongruente Mengen", Portugal. Math. 4: 238–242 .
• Hadwiger, Hugo (1961), "Ungelöste Probleme No. 40", Elem. Math. 16: 103–104 .
• Jensen, Tommy R.; Toft, Bjarne (1995), Graph Coloring Problems, Wiley-Interscience Series in Discrete Mathematics and Optimization, pp. 150–152 .
• Shelah, Saharon; Soifer, Alexander (2003), "Axiom of choice and chromatic number of the plane", Journal of Combinatorial Theory, Series A 103 (2): 387–391, doi:10.1016/S0097-3165(03)00102-X, http://www.uccs.edu/~faculty/asoifer/docs/AXIOMOFCHOICEinJCT.pdf .
• Soifer, Alexander (2008), The Mathematical Coloring Book: Mathematics of Coloring and the Colorful Life of its Creators, New York: Springer, ISBN 978-0387746401 

External links

• O'Rourke, Joseph. "Problem 57: Chromatic Number of the Plane". The Open Problems Project. http://maven.smith.edu/~orourke/TOPP/P57.html. 
• Mohar, Bojan (2001). "The chromatic number of the Unit Distance Graph". http://www.fmf.uni-lj.si/~mohar/Problems/P8UnitDistanceGraph.html. 
• Radoičić, Radoš; Tóth, Géza. "Note on the chromatic number of the space". http://www.math.rutgers.edu/~rados/chromnumber.ps.