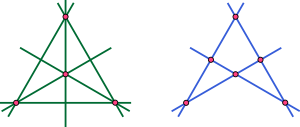
Complete quadrangle

A complete quadrangle (at left) and a complete quadrilateral (at right).

In mathematics, specifically projective geometry, a complete quadrangle is a system of geometric objects consisting of any four points in the Euclidean plane, no three of which are on a common line, and of the six lines connecting each pair of points. Dually, a complete quadrilateral is a system of four lines, no three of which pass through the same point, and the six points of intersection of these lines. The complete quadrangle was called a tetrastigm by Lachlan (1893), and the complete quadrilateral was called a tetragram; those terms are occasionally still used.

Diagonals

The six lines of a complete quadrangle meet in pairs to form three additional points called the diagonal points of the quadrangle. Similarly, among the six points of a complete quadrilateral there are three pairs of points that are not already connected by lines; the line segments connecting these pairs are called diagonals. Since the discovery of the Fano plane, a non-Euclidean geometry in which the diagonal points of a complete quadrangle are collinear, it has become necessary to augment the axioms of projective geometry with Fano's axiom that the diagonal points are not collinear.^[1]

Projective properties

As systems of points and lines in which all points belong to the same number of lines and all lines contain the same number of points, the complete quadrangle and the complete quadrilateral both form projective configurations; in the notation of projective configurations, the complete quadrangle is written as (4₃6₂) and the complete quadrilateral is written (6₂4₃), where the numbers in this notation refer to the numbers of points, lines per point, lines, and points per line of the configuration. The projective dual of a complete quadrangle is a complete quadrilateral, and vice versa. For any two complete quadrangles, or any two complete quadrilaterals, there is a unique projective transformation taking one of the two configurations into the other.^[2]

Euclidean properties

Wells (1991) describes several additional properties of complete quadrilaterals that involve metric properties of the Euclidean plane, rather than being purely projective. The midpoints of the diagonals are collinear, and (as proved by Isaac Newton) also collinear with the center of a conic that is tangent to all four lines of the quadrilateral. Any three of the lines of the quadrilateral form the sides of a triangle; the orthocenters of the four triangles formed in this way lie on a second line, perpendicular to the one through the midpoints. The circumcircles of these same four triangles meet in a point. In addition, the three circles having the diagonals as diameters belong to a common pencil of circles^[3] the axis of which is the line through the orthocenters.

Notes

1. ^ Hartshorne 1967; Coxeter 1987, p. 15.
2. ^ Coxeter 1987, p. 51
3. ^ Wells writes incorrectly that the three circles meet in a pair of points, but, as can be seen in Bogomolny's animation of the same results, the pencil can be hyperbolic instead of elliptic, in which case the circles do not intersect.

References

• Coxeter, H. S. M. (1987). Projective Geometry, 2nd ed.. Springer-Verlag. ISBN 0-387-96532-7. 
• Hartshorne, Robin (1967). Foundations of Projective Geometry. W. A. Benjamin. pp. 53—6. 
• Lachlan, R. (1893). "Properties of a Tetrastigm.". An Elementary Treatise on Modern Pure Geometry. London: Macmillan. pp. 85–90. 
• Wells, David (1991). The Penguin Dictionary of Curious and Interesting Geometry. Penguin. pp. 35–36. ISBN 0-14-011813-6. 

External links

• Bogomolny, Alexander. "The Complete Quadrilateral". Cut-the-Knot. http://www.cut-the-knot.org/ctk/CompleteQuadrilateral.shtml. 
• Weisstein, Eric W., "Complete Quadrangle" from MathWorld.