- Saros (astronomy)
-
The saros
 i/ˈsɛərɒs/ is a a period of 223 synodic months (approximately 6585.3213 days, or nearly 18 years 11 days), that can be used to predict eclipses of the Sun and Moon. One saros after an eclipse, the Sun, Earth, and Moon return to approximately the same relative geometry, and a nearly identical eclipse will occur, in what is referred to as an eclipse cycle. A sar is one half of a saros.
i/ˈsɛərɒs/ is a a period of 223 synodic months (approximately 6585.3213 days, or nearly 18 years 11 days), that can be used to predict eclipses of the Sun and Moon. One saros after an eclipse, the Sun, Earth, and Moon return to approximately the same relative geometry, and a nearly identical eclipse will occur, in what is referred to as an eclipse cycle. A sar is one half of a saros.A series of eclipses that are separated by one saros is called a saros series.
Contents
History
The earliest discovered historical record of the saros is by the Chaldeans (ancient Babylonian astronomers) in the last several centuries BC,[1][2][3] and was later known to Hipparchus, Pliny[4] and Ptolemy,[5] but under different names. The Sumerian/Babylonian word "šár" was one of the ancient Mesopotamian units of measurement and as a number appears to have had a value of 3600.[6] The name "saros" (Greek: σάρος) was first given to the eclipse cycle by Edmond Halley in 1691, who took it from the Suda, a Byzantine lexicon of the 11th century.[7] The information in the Suda in turn was derived directly or otherwise from the Chronicle of Eusebius of Caesarea, which quoted Berossus. Although Halley's naming error was pointed out by Guillaume Le Gentil in 1756, the name continues to be used.
Description
The saros, a period of 6585.322 days (14 normal years + 4 leap years + 11.322 days, or 13 normal years + 5 leap years + 10.322 days), is useful for predicting the times at which nearly identical eclipses will occur, and derives from three periodicities of the lunar orbit: the synodic month, the draconic month, and the anomalistic month. For an eclipse to occur, either the Moon must be located between the Earth and Sun (for a solar eclipse) or the Earth must be located between the Sun and Moon (for a lunar eclipse). This can happen only when the Moon is new or full, respectively, and repeat occurrences of these lunar phases are controlled by the Moon's synodic period, which is about 29.53 days. Most of the times during a full and new moon, however, the shadow of the Earth or Moon falls to the north or south of the other body. Thus, if an eclipse is to occur, the three bodies must also be nearly in a straight line. This condition occurs only when a full or new Moon passes close to the ecliptic plane (during an eclipse season) which is the case around the time when it passes through one of the two nodes of its orbit (the ascending or descending node). The period of time for two successive passes through the ecliptic plane at the same node is given by the draconic month, which is 27.21 days. So the conditions of an eclipse are met when the new or full moon is near one of the nodes, which occurs every 5 or 6 months (the Sun, being in conjunction or opposition to the Moon, is also at a node of the Moon's orbit at that time - this happens twice in an eclipse year). However, if two eclipses are to have the same appearance and duration, then also the distance between the Earth and Moon, as well as the Earth and Sun, must be the same for both events. The time it takes the Moon to orbit the Earth once and return to the same distance is given by the anomalistic month, which has a period of 27.55 days.
The origin of the saros comes from the recognition that 223 synodic months is approximately equal to 242 draconic months, which is approximately equal to 239 anomalistic months (this approximation is good to within about 2 hours). After one saros, the Moon will have completed roughly an integer number of synodic, draconic, and anomalistic months, and the Earth-Sun-Moon geometry will be nearly identical: the Moon will have the same phase, be at the same node, and have the same distance from the Earth. In addition, because the saros is close to 18 years in length (about 11 days longer), the earth will be nearly the same distance from the sun, and tilted to it in nearly the same orientation (same season).[8] If one knew the date of an eclipse, then one saros later, a nearly identical eclipse should occur. Note that during this 18-year cycle, about 40 other solar and lunar eclipses take place, but with a somewhat different geometry. Note also that the saros (18.03 years) is not equal to an integer number of revolutions of the Moon with respect to the fixed stars (sidereal month of 27.32 days). Therefore, even though the relative geometry of the Earth-Sun-Moon system will be nearly identical after a saros, the Moon will be in a different position with respect to the stars. This is due to the fact that the orbit of the Moon precesses.
A complication with the saros is that its period is not an integer number of days, but contains a multiple of ⅓ of a day. Thus, as a result of the Earth's rotation, for each successive saros, an eclipse will occur about 8 hours later in the day. In the case of an eclipse of the Sun, this means that the region of visibility will shift westward by 120°, or one third of the way around the globe, and the two eclipses will thus not be visible from the same place on Earth. In the case of an eclipse of the Moon, the next eclipse might still be visible from the same location as long as the Moon is above the horizon. However, if one waits three saros, the local time of day of an eclipse will be nearly the same. This period of three saros (54 years 1 month, or almost 19756 full days), is known as a triple saros or exeligmos (Greek: "turn of the wheel").
Saros series
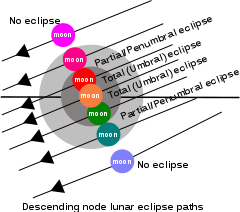
The saros is based on the recognition that 223 synodic months approximately equal to 242 draconic months and 239 anomalistic months. However, as this relationship is not perfect, the geometry of two eclipses separated by one saros will differ slightly. In particular, the place where the Sun and Moon come in conjunction shifts westward by about 0.5° with respect to the Moon's nodes every saros, and this gives rise to a series of eclipses, called a saros series, that slowly change in appearance.
Each saros series starts with a partial eclipse (Sun first enters the end of the node), and each successive saros the path of the Moon is shifted either northward (when near the descending node) or southward (when near the ascending node). At some point, eclipses are no longer possible and the series terminates (Sun leaves the beginning of the node). Arbitrary dates were established by compilers of eclipse statistics. These extreme dates are 2000 BCE and 3000 CE. Saros series, of course, went on before and will continue after these dates. Since the first eclipse of 2000 BCE was not the first in its saros, it is necessary to extend the saros series numbers backwards beyond 0 to negative numbers to accommodate eclipses occurring in the years following 2000 BCE. The saros -13 is the first saros to appear in these data. For solar eclipses the statistics for the complete saros series within the era between 2000 BCE and 3000 CE are given in this article's references.[9][10] It takes between 1226 and 1550 years for the members of a saros series to traverse the Earth's surface from north to south (or vice-versa). These extremes allow from 69 to 87 eclipses in each series (most series have 71 or 72 eclipses). From 39 to 59 (mostly about 43) eclipses in a given series will be central (that is, total, annular, or hybrid annular-total). At any given time, approximately 40 different saros series will be in progress.
Saros series are numbered according to the type of eclipse (solar or lunar) and whether they occur at the Moon's ascending or descending node.[11][12] Odd numbers are used for solar eclipses occurring near the ascending node, whereas even numbers are given to descending node solar eclipses. For lunar eclipses, this numbering scheme is somewhat random. The ordering of these series is determined by the time at which each series peaks, which corresponds to when an eclipse is closest to one of the lunar nodes. For solar eclipses, (in 2003) the 39 series numbered between 117 and 155 are active, whereas for lunar eclipses, there are now 41 active saros series.[citation needed]
Example: Lunar saros 131
Saros 131 lunar eclipse dates May 10, 1427
(Julian calendar)First penumbral
(southern edge of shadow)...6 intervening penumbral eclipses omitted... July 25, 1553
(Julian calendar)First partial ...19 intervening partial eclipses omitted... March 22, 1932
Final partial12:32 UT April 2, 1950
First total20:44 UT 
April 13, 1968 04:47 UT April 24, 1986 12:43 UT May 4, 2004 20:30 UT May 16, 2022
First central04:11 UT 
May 26, 2040 11:45 UT June 6, 2058 19:14 UT June 17, 2076
Central02:37 UT 
...6 intervening total eclipses omitted... September 3, 2202
Last total05:59 UT September 13, 2220
First partial...18 intervening partial eclipses omitted... April 9, 2563 Last partial umbral ...7 intervening penumbral eclipses omitted... July 7, 2707 Last penumbral
(northern edge of shadow)As an example of a single saros series, the accompanying table gives the dates of some of the 72 lunar eclipses for saros series 131. This eclipse series began in AD 1427 with a partial eclipse at the southern edge of the Earth's shadow when the Moon was close to its descending node. Each successive saros, the Moon's orbital path is shifted northward with respect to the Earth's shadow, with the first total eclipse occurring in 1950. For the following 252 years, total eclipses occur, with the central eclipse being predicted to occur in 2078. The first partial eclipse after this is predicted to occur in the year 2220, and the final partial eclipse of the series will occur in 2707. The total lifetime of the lunar saros series 131 is 1280 years.
Because of the ⅓ fraction of days in a saros, the visibility of each eclipse will differ for an observer at a given locale. For the lunar saros series 131, the first total eclipse of 1950 had its best visibility for viewers in Eastern Europe and the Middle East because mid-eclipse was at 20:44 UT. The following eclipse in the series occurred approximately 8 hours later in the day with mid-eclipse at 4:47 UT, and was best seen from North America and South America. The third total eclipse occurred approximately 8 hours later in the day than the second eclipse with mid-eclipse at 12:43 UT, and had its best visibility for viewers in the Western Pacific, East Asia, Australia and New Zealand. This cycle of visibility repeats from the initiation to termination of the series, with minor variations.
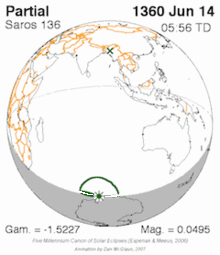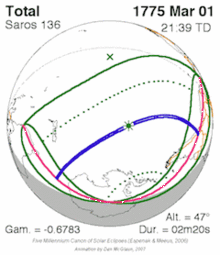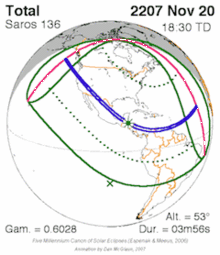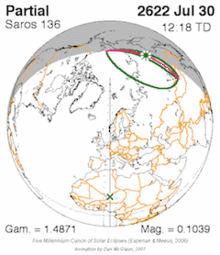
For a similar example for solar saros see solar saros 136.
Relationship between lunar and solar saros (sar)
After a given lunar or solar eclipse, after 9 years and 5.5 days (a half saros) an eclipse will occur that is lunar instead of solar, or vice versa, with similar properties. For example if the moon's penumbra partially covers the southern limb of the earth during a solar eclipse, 9 years and 5.5 days later a lunar eclipse will occur in which the moon is partially covered by the southern limb of the earth's penumbra. Likewise, 9 years and 5.5 days after a total solar eclipse occurs, a total lunar eclipse will also occur. This 9 year period is referred to as a sar. It includes 111.5 synodic months, or 111 synodic months plus one fortnight. The fortnight accounts for the alternation between solar and lunar eclipse. For a visual example see this chart (each row is one sar apart).
See also
References
Cited references
- ^ Tablets 1414, 1415, 1416, 1417, 1419 of: T.G. Pinches, J.N. Strassmaier: Late Babylonian Astronomical and Related Texts. A.J. Sachs (ed.), Brown University Press 1955
- ^ A.J. Sachs & H. Hunger (1987..1996): Astronomical Diaries and Related Texts from Babylonia, Vol.I..III. Österreichischen Akademie der Wissenschaften. ibid. H. Hunger (2001) Vol. V: Lunar and Planetary Texts
- ^ P.J. Huber & S de Meis (2004): Babylonian Eclipse Observations from 750 BC to 1 BC, par. 1.1. IsIAO/Mimesis, Milano
- ^ Naturalis Historia II.10[56]
- ^ Almagest IV.2
- ^ Microsoft Encarta College Dictionary, 2001
- ^ The Suda entry is online here.
- ^ Littmann, Mark; Fred Espenak, Ken Willcox (2008). Totality: Eclipses of the Sun. Oxford University Press. ISBN 0199532095.
- ^ Meeus, Jean (2004). Ch. 18 "About Saros and Inex series" in: Mathematical Astronomy Morsels III. Willmann-Bell, Richmond VA, USA.
- ^ Espenak, Fred; Jean Meeus (October 2006). "Five Millennium Canon of Solar Eclipses, Section 4 (NASA TP-2006-214141)" (PDF). NASA STI Program Office. http://sunearth.gsfc.nasa.gov/eclipse/5MCSE/5MCSE-Text.pdf. Retrieved 2007-01-24.
- ^ G. van den Bergh (1955). Periodicity and Variation of Solar (and Lunar) Eclipses (2 vols.). H.D. Tjeenk Willink & Zoon N.V., Haarlem.
- ^ Bao-Lin Liu and Alan D. Fiala (1992). Canon of Lunar Eclipses, 1500 B.C. to A.D. 3000. Willmann-Bell, Richmond VA.
General references
- Jean Meeus and Hermann Mucke (1983) Canon of Lunar Eclipses. Astronomisches Büro, Vienna
- Theodor von Oppolzer (1887). Canon der Finsternisse. Vienna
- Mathematical Astronomy Morsels, Jean Meeus, Willmann-Bell, Inc., 1997 (Chapter 9, p. 51, Table 9.A Some eclipse Periodicities)
External links
- NASA - Eclipses and the Saros
- NASA - Catalog of Lunar Eclipses in Saros 0
- NASA - Lunar Eclipses of Saros Series 1 to 180
- NASA - Solar Eclipses of Saros Series 0 to 180
- NASA - Summary of Lunar Eclipses in Saros Series -20 to 183
- NASA - Summary of Solar Eclipses in Saros Series -13 to 190
- Search among the 11,898 solar eclipses over five millennium and display interactive maps
- Search among the 12,064 lunar eclipses over five millennium and display interactive maps
- Eclipses and the Saros Cycle
- Eclipse Search -- here one can search 5,000 years of eclipse data by type, magnitude, Saros number or simply by year.
- Saros series 131 table
Solar eclipses Lists of
eclipsesAntiquity · 20th century BC • 19th century BC • 18th century BC • 17th century BC • 16th century BC • 15th century BC • 14th century BC • 13th century BC • 12th century BC • 11th century BC • 10th century BC • 9th century BC • 8th century BC • 7th century BC • 6th century BC • 5th century BC • 4th century BC • 3rd century BC • 2nd century BC • 1st century BC • 1st century · 2nd century · 3rd century · 4th century · 5th century · 6th century · 7th century · 8th century · 9th century · 10th century · 11th century · 12th century · 13th century · 14th century · 15th century · 16th century · 17th century · 18th century · 19th century · 20th century · 21st century · 22nd century · 23rd century · 24th century · 25th century · 26th century · 27th century · 28th century · 29th century · 30th century
Eclipses seen from: China · the United Kingdom · Philippines
Saros series: 110 · 111 · 112 · 113 · 114 · 115 · 116 · 117 · 118 · 119 · 120 · 121 · 122 · 123 · 124 · 125 · 126 · 127 · 128 · 129 · 130 · 131 · 132 · 133 · 134 · 135 · 136 · 137 · 138 · 139 · 140 · 141 · 142 · 143 · 144 · 145 · 146 · 147 · 148 · 149 · 150 · 151 · 152 · 153 · 154 · 155 · 156 · 157 · 158 · 159 · 160 · 161 · 162

Historical
eclipsesMursili's eclipse (1312 BC) · Assyrian eclipse (763 BC) · Battle of Halys (585 BC) · Crucifixion darkness and eclipse 1560 Aug 21 · 1598 Mar 7 · 1652 Apr 8 · 1654 Aug 12 · 1699 Sep 23 · 1715 May 3 · 1724 May 22 · 1766 Feb 9 · 1778 Jun 24 · 1780 Oct 27 · 1806 Jun 16 · 1816 Nov 19 · 1820 Sep 7 · 1824 Jun 26 · 1842 Jul 8 · 1851 Jul 28 · 1853 Nov 30 · 1857 Mar 25 · 1858 Sep 7 · 1860 Jul 18 · 1865 Apr 25 · 1867 Aug 29 · 1868 Aug 18 · 1869 Aug 7 · 1870 Dec 22 · 1871 Dec 12 · 1874 Apr 16 · 1875 Apr 6 · 1878 Jul 29 · 1882 May 17 · 1883 May 6 · 1885 Sep 8 · 1886 Aug 29 · 1887 Aug 19 · 1889 Jan 1 · 1889 Dec 22 · 1893 Apr 16 · 1896 Aug 9 · 1898 Jan 22 · 1919 May 29
Past
Total/hybrid
eclipses1970 Mar 7 · 1972 Jul 10 · 1973 Jun 30 · 1974 Jun 20 · 1976 Oct 23 · 1977 Oct 12 · 1979 Feb 26 · 1980 Feb 16 · 1981 Jul 31 · 1983 Jun 11 · 1984 Nov 22 · 1985 Nov 12 · 1986 Oct 3 · 1987 Mar 29 · 1988 Mar 18 · 1990 Jul 22 · 1991 Jul 11 · 1992 Jun 30 · 1994 Nov 3 · 1995 Oct 24 · 1997 Mar 9 · 1998 Feb 26 · 1999 Aug 11 · 2001 Jun 21 · 2002 Dec 4 · 2003 Nov 23 · 2005 Apr 8 · 2006 Mar 29 · 2008 Aug 1 · 2009 Jul 22 · 2010 Jul 11
Future
Total/hybrid
eclipses2012 Nov 13 · 2013 Nov 3 · 2015 Mar 20 · 2016 Mar 9 · 2017 Aug 21 · 2019 Jul 2 · 2020 Dec 14 · 2021 Dec 4 · 2023 Apr 20 · 2024 Apr 8 · 2026 Aug 12 · 2027 Aug 2 · 2028 Jul 22 · 2030 Nov 25 · 2031 Nov 14 · 2033 Mar 30 · 2034 Mar 20 · 2035 Sep 2 · 2037 Jul 13 · 2038 Dec 26 · 2039 Dec 15 · 2041 Apr 30 · 2042 Apr 20 · 2043 Apr 9 · 2044 Aug 23 · 2045 Aug 12 · 2046 Aug 2 · 2048 Dec 5 · 2049 Nov 25 ·
Past
Annular
eclipses1970 Aug 31 · 1972 Jan 16 · 1973 Jan 4 · 1973 Dec 24 · 1976 Apr 29 · 1977 Apr 18 · 1979 Aug 22 · 1980 Aug 10 · 1981 Feb 4 · 1983 Dec 4 · 1984 May 30 · 1987 Sep 23 · 1988 Sep 11 · 1990 Jan 26 · 1991 Jan 15 · 1992 Jan 4 · 1994 May 10 · 1995 Apr 29 · 1998 Aug 22 · 1999 Feb 16 · 2001 Dec 14 · 2002 Jun 10 · 2003 May 31 · 2005 Oct 3 · 2006 Sep 22 · 2008 Feb 7 · 2009 Jan 26 · 2010 Jan 15
Future
Annular
eclipses2012 May 20 · 2013 May 10 · 2014 Apr 29 · 2016 Sep 1 · 2017 Feb 26 · 2019 Dec 26 · 2020 Jun 21 · 2021 Jun 10 · 2023 Oct 14 · 2024 Oct 2 · 2026 Feb 17 · 2027 Feb 6 · 2028 Jan 26 · 2030 Jun 1 · 2031 May 21 · 2032 May 9 · 2034 Sep 12 · 2035 Mar 9 · 2038 Jan 5 · 2038 Jul 2 · 2039 Jun 21 · 2041 Oct 25 · 2042 Oct 14 · 2043 Oct 3 · 2044 Feb 28 · 2045 Feb 16 · 2046 Feb 5 · 2048 Jun 11 · 2049 May 31 ·
Other
planetsRelated
topicsLunar eclipses Lists of
eclipsesAll: Central total eclipses · Total penumbral eclipses
By century: 20th BCE · 19th BCE · 18th BCE · 17th BCE · 16th BCE · 15th BCE · 14th BCE · 13th BCE · 12th BCE · 11th BCE · 10th BCE · 9th BCE · 8th BCE · 7th BCE · 6th BCE · 5th BCE · 4th BCE · 3rd BCE · 2nd BCE · 1st BCE · 1st · 2nd · 3rd · 4th · 5th · 6th · 7th · 8th · 9th · 10th · 11th · 12th · 13th · 14th · 15th · 16th · 17th · 18th · 19th · 20th · 21st · 22nd · 23rd · 24th · 25th · 26th · 27th · 28th · 29th · 30th
Saros cycles: 100 · 101 · 102 · 103 · 104 · 105 · 106 · 107 · 108 · 109 · 110 · 111 · 112 · 113 · 114 · 115 · 116 · 117 · 118 · 119 · 120 · 121 · 122 · 123 · 124 · 125 · 126 · 127 · 128 · 129 · 130 · 131 · 132 · 133 · 134 · 135 · 136 · 137 · 138 · 139 · 140 · 141 · 142 · 143 · 144 · 145 · 146 · 147 · 148 · 149 · 150 · 151 · 152 · 153 · 154 · 155 · 156 · 157 · 158 · 169 · 160 · 161 · 162 · 163
Total
eclipsesPast1910 May 24 · 1913 Sep 15 · 1920 May 03 · 1921 Apr 22 · 1928 Jun 3 · 1939 May 3 · 1946 Jun 14 · 1950 Apr 2 · 1953 Jan 29 · 1953 Jul 26 · 1954 Jan 19 · 1956 Nov 18 · 1957 May 13 · 1957 Nov 7 · 1960 Mar 13 · 1960 Sep 5 · 1963 Dec 30 · 1964 Jun 25 · 1964 Dec 19 · 1967 Apr 24 · 1967 Oct 18 · 1968 Apr 13 · 1968 Oct 6 · 1971 Feb 10 · 1971 Aug 6 · 1972 Jan 30 · 1974 Nov 29 · 1975 May 25 · 1975 Nov 18 · 1978 Mar 24 · 1978 Sep 16 · 1979 Sep 6 · 1982 Jan 9 · 1982 Jul 6 · 1982 Dec 30 · 1985 May 4 · 1985 Oct 28 · 1986 Apr 24 · 1986 Oct 17 · 1989 Feb 20 · 1989 Aug 17 · 1990 Feb 9 · 1992 Dec 9 · 1993 Jun 4 · 1993 Nov 29 · 1996 Apr 4 · 1996 Sep 27 · 1997 Sep 16 · 2000 Jan 21 · 2000 Jul 16 · 2001 Jan 9 · 2003 May 16 · 2003 Nov 9 · 2004 May 4 · 2004 Oct 28 · 2007 Mar 3 · 2007 Aug 28 · 2008 Feb 21 · 2010 Dec 21 · 2011 Jun 15
Future2011 Dec 10 · 2014 Apr 15 · 2014 Oct 8 · 2015 Apr 4 · 2015 Sep 28 · 2018 Jan 31 · 2018 Jul 27 · 2019 Jan 21 · 2021 May 26 · 2022 May 16 · 2022 Nov 8 · 2025 Mar 14 · 2025 Sep 7 · 2026 Mar 3 · 2028 Dec 31 · 2029 Jun 26 · 2029 Dec 20 · 2032 Apr 25 · 2032 Oct 18 · 2033 Apr 14 · 2033 Oct 8 · 2036 Feb 11 · 2036 Aug 7 · 2037 Jan 31 · 2040 May 26 · 2040 Nov 18 · 2043 Mar 25 · 2043 Sep 19 · 2044 Mar 13 · 2044 Sep 7 · 2047 Jan 12 · 2047 Jul 7 · 2048 Jan 1 · 2050 May 6 · 2050 Oct 30
Partial
eclipsesPast1903 Apr 12 · 1914 Mar 12 · 1932 Mar 22 · 1952 Feb 11 · 1952 Aug 5 · 1954 Jul 16 · 1955 Nov 29 · 1956 May 24 · 1958 May 3 · 1959 Mar 24 · 1961 Mar 2 · 1961 Aug 26 · 1963 Jul 6 · 1965 Jun 14 · 1970 Feb 21 · 1970 Aug 17 · 1972 Jul 26 · 1973 Dec 10 · 1974 Jun 4 · 1976 May 13 · 1977 Apr 4 · 1979 Mar 13 · 1981 Jul 17 · 1983 Jun 25 · 1988 Mar 3 · 1988 Aug 27 · 1990 Aug 6 · 1991 Dec 21 · 1992 Jun 15 · 1994 May 25 · 1995 Apr 15 · 1997 Mar 24 · 1999 Jul 28 · 2001 Jul 5 · 2005 Oct 17 · 2006 Sep 7 · 2008 Aug 16 · 2009 Dec 31 · 2010 Jun 26
Future2012 Jun 4 · 2013 Apr 25 · 2017 Aug 7 · 2019 Jul 16 · 2021 Nov 19 · 2023 Oct 28 · 2024 Sep 18 · 2026 Aug 28 · 2028 Jan 12 · 2028 Jul 6 · 2030 Jun 15 · 2034 Sep 28 · 2035 Aug 19 · 2037 Jul 27 · 2039 Jun 6 · 2039 Nov 30 · 2041 May 16 · 2041 Nov 8 · 2042 Sep 29 · 2046 Jan 22 · 2046 Jul 18 · 2048 Jun 26
Categories:- Eclipses
- Time in astronomy
- Technical factors of astrology
Wikimedia Foundation. 2010.