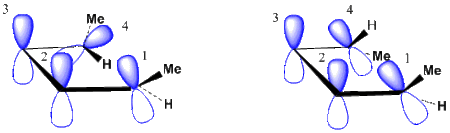Möbius–Hückel concept

The Möbius-Hückel treatment is one of two predicting reaction allowedness versus forbiddeness. The concept is the counterpart of the Woodward-Hoffmann approach. The methodology in this treatment utilizes the plus-minus sign parity in proceeding around a cycle of orbitals in a molecule or reaction while the Woodward-Hoffmann methodology uses a large number of rules with the same consequences.

Introduction

The Möbius-Hückel (M-H) Concept for reaction allowedness and forbiddeness. One year following the Woodward Hoffmann^[1] and Longuet-Higgins^[2] publications, it was noted by Zimmerman that both transition states and stable molecules sometimes involved a Möbius array of basis orbitals^[3][4] The Möbius–Hückel treatment provides an alternative to the Woodward-Hoffmann one. In contrast to the Woodward-Hoffmann approach the Möbius-Hückel treatment is not dependent on symmetry and only requires counting the number of plus-minus sign inversions in proceeding around the cyclic array of orbitals. Where one has zero or an even number of sign inversions there is a Hückel array. Where an odd-number of sign inversions is found a Möbius array is determined to be present. Thus the approach goes beyond the geometric consideration of Edgar Heilbronner. In any case, symmetry may be present or may not.

Edgar Heilbronner had described twisted annulenes which had Möbius topology, but in including the twist of these systems, he concluded that Möbius systems could never be lower in energy than the Hückel counterparts.^[5] In contrast, the Möbius-Hückel (M-H) Concept considers systems with an equal twist for Hückel and Möbius Systems.

The Theory and Concept

For Möbius Systems there is an odd number of plus-minus sign inversions in the basis set in proceeding around the cycle. A circle mnemonic^[3] was advanced which provides the MO energies of the system; this was the counterpart of the Frost-Musulin mnemonic^[6] for ordinary Hückel systems. It was concluded that 4N electrons is the preferred number for Möbius moieties in contrast to the common 4N+2 electrons for ordinary Hückel systems.

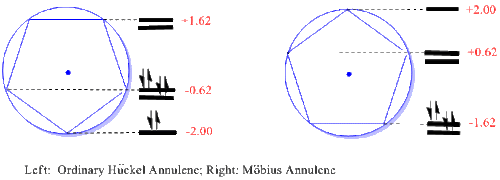
The Möbius-Hückel Circle Mnemonic

The Möbius-Hückel Circle Mnemonic^[3] Applied to the Example of Cyclopentadienyl

The cyclopentadienyl annulenes are used here as an example; but in general whatever cyclic annulene is desired is inscribed in the circle of radius 2 beta and centered at zero (the energy of an isolated p-orbital). For every intersection of the annulene with the circle a molecular orbital energy is predicted at that vertical displacement. For Hückel Systems the vertex is positioned at the circle bottom at suggested by Frost. But for Möbius systems a polygon side is positioned at the circle bottom. It is seen that with one MO at the bottom and then groups of degenerate pairs, the Hückel Systems will accommodate 4N+2 electrons, following the ordinary Hückel rule. However, in contrast, the Möbius Systems have degenerate pairs of MO's starting at the circle bottom and thus will accommodate 4N electrons. For cyclic annulenes one then predicts which species will be favored. The method applies equally to cyclic reaction intermediates and transition states.

Application to Molecules and Pericyclic Reactions

Thus it was noted that along the reaction coordinate of pericyclic processes one could have either a Möbius or a Hückel array of basis orbitals. With 4N or 4N+2 electrons, one is then led to a prediction of allowedness or forbiddeness. Additionally, the M-H mnemonics give the MO’s at part reaction. At each degeneracy there is a crossing of MO’s. Thus one can determine if the highest occupied MO becomes anti-bonding with a forbidden reaction resulting. Finally, the M-H parity of sign inversions was utilized in the 1970 W-H treatment of alloweness-forbiddeness. The parity of sign inversions between bonds and atoms was used in place of the M-H use of atoms; the two approaches are equivalent.^[7]

Simple Tabular Correlation of Allowedness-Forbiddeness of Möbius versus Hückel and 4n+2 versus 4N Electrons

The table in Figure 2 summarizes the Möbius–Hückel concept. The columns specify whether one has a Möbius or a Hückel structure and the rows specify whether 4N+2 electrons or 4N electrons are present. Depending on which is present, a Möbius or a Hückel system, one selects the first or the second column. Then depending on the number of electrons present, 4N+2 or 4N, one selects the first or the second row.^[7]

Figure 2.Prediction of Allowed vs Forbidden Reactions; Aromatic vs Anti-Aromatic Molecules

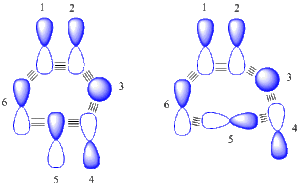
The generalized Möbius-Hückel orbital arrays; Recognizing each variety

The two orbital arrays in Figure 3 are just examples and do not correspond to real systems. In inspecting the Möbius one on the left, plus-minus overlaps are seen between orbital pairs 2-3, 3-4, 4-5, 5-6 and 6-1, corresponding to an odd number 5 as required by a Möbius system. Inspection of the Hückel one on the right, plus-minus overlaps are seen between orbital pairs 2-3, 3-4, 4-5, and 6-1, corresponding to an even number 4 as required by a Hückel system.

The plus-minus orientation of each orbital is arbitrary since these are just basis set orbitals and do not correspond to any molecular orbital. If any orbital were to change signs, two plus-minus overlaps are either removed or added and the parity (even vs oddness) is not changed. One choice of signs leads to zero plus-minus overlaps for the Hückel array on the right.

Figure 3. Möbius and Hückel Orbital Arrays (Möbius Left and Hückel Right)

The Butadiene to Cyclobutene example

Figure 4 shows the orbital array involved in the butadiene to cyclobutene interconversion. It is seen that there are four orbitals in this cyclic array. Thus in the interconversion reactions orbitals 1 and 4 overlap either in a conrotatory or a disrotatory fashion. Also, it is seen that the conrotation involves one plus-minus overlap as drawn while the disrotation involves zero plus-minus overlaps as drawn. Thus the conrotation uses a Möbius array while the disrotation uses a Hückel array.^[3]

Figure 4. Butadiene - Cyclobutene interconversion; Disrotation (Hückel) Left, Conrotation (Möbius) Right.

But it is important to note, as described for the generalized orbital array in Figure 3,that the assignment of the basis-set p-orbitals is arbitrary. Were one p-orbital in either reaction mode to be written upside-down, this would change the number of sign inversions by two and not change the evenness or oddness of the orbital array.

With a conrotation giving a Möbius system, with butadiene's four electrons, we find an "allowed" reaction model. With disrotation giving a Hückel system, with the four electrons, we find a "forbidden" reaction model.

Although in these two examples symmetry is present, symmetry is not required or involved in determination of reaction allowedness versus forbiddeness. Hence a very large number of organic reactions can be understood. Even where symmetry is present, the Möbius-Hückel analysis proves simple to employ.

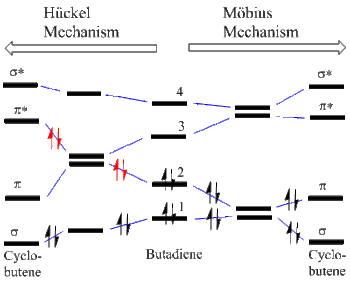
MO Degeneracies Leading to Correlation Diagrams

It has been noted that for every degeneracy along a reaction coordinate there is a molecular orbital crossing.^[4] Thus for the butadiene to cyclobutene conversion, the two Möbius (here Conrotatory) and Hückel (here Disrotatory) modes are shown in Figure 5. The starting MO's are depicted in the center of the correlation diagram with blue correlation lines connecting MO's. It is seen that for the Möbius mode the four electrons in MO's 1 and 2 end in the bonding MO's (i.e. sigma and pi) of cyclobutene. In contrast, for the Hückel mode, there is a degeneracy and thus an MO crossing leading to two electrons (drawn in red)are headed for an antibonding MO. Thus the Hückel mode is Forbidden while the Möbius mode is Allowed.

One further relevant point is that the first organic correlation diagrams were in a 1961 publication on carbanion rearrangements.^[8] It had been noted that when an occupied molecular orbital becomes antibonding the reaction is inhibited and this phenomenon was correlated with a series of rearrangements.

Figure 5. Möbius-Hückel Correlation Diagram; Two Modes of Butadiene to Cyclobutene Conversion

The Relation of the Möbius-Hückel concept to the Woodward-Hoffmann methods

Until 1969 there was no obvious relationship except that the two methods lead to the same predictions. As noted earlier, the Woodward-Hoffmann method requires symmetry. But in 1969 and 1970 a “General Formulation” was published^[9][10], namely, A ground-state pericyclic change is symmetry-allowed when the total number of (4q+2)_s and (4r)_a components is odd. The 1969-1970 Woodward-Hoffmann General Formulation is seen to be equivalent to the Zimmerman Möbius-Hückel concept. Thus each (4r)_a component provides one plus-minus overlap in the cyclic array (i.e. an odd number) for 4n electrons. The (4q + 2)_s component just makes certain that the number of electrons in symmetric bonds is 4n+2.

The equivalency of the more recent formulation of the Woodward-Hoffmann rules has been discussed^[11].

References

1. ^ “Stereochemistry of electrocyclic reactions”, Woodward, R. B.; Hoffmann, Roald. J. Amer. Chem. Soc. 1965, 87, 395-397.
2. ^ "The Electronic Mechanism of Electrocyclic Reactions" Longuet-Higgins, H. C.; Abrahamson, E. W. J. Am. Chem. Soc., 1965, 87, 2045-2046.
3. ^ ^{a b c d} "On Molecular Orbital Correlation Diagrams, the Occurrence of Möbius Systems in Cyclization Reactions, and Factors Controlling Ground and Excited State Reactions. I," Zimmerman, H. E. J. Am. Chem. Soc., 1966, 88, 1564-1565.
4. ^ ^{a b} "On Molecular Orbital Correlation Diagrams, Möbius Systems, and Factors Controlling Ground and Excited State Reactions. II," Zimmerman, H. E. J. Am. Chem. Soc., 1966, 88, 1566-1567.
5. ^ "Hueckel molecular orbitals of Moebius-type conformations of annulenes," Heilbronner, E. Tetrahedron Letts 1964, 1923-1928.
6. ^ Frost, A. A.; Musulin, B. "Mnemonic device for molecular-orbital energies." J. Chem. Phys. 1953, 21 572-573.
7. ^ ^{a b} "The Möbius-Hückel Concept in Organic Chemistry. Application to Organic Molecules and Reactions," Zimmerman, H. E. Acc. Chem. Res., 1971, 4, 272-280.
8. ^ "Carbanion Rearrangements. II," Zimmerman, H. E.; Zweig, A. J Am. Chem. Soc., 1961, 83, 1196-1213.
9. ^ Woodward, R.B; Hoffmann, R., "Conservation of Orbital Symmetry" Angew. Chem. 1969, 81, 781-932.
10. ^ Woodward, R. B.; Hoffmann, R., “Conservation of Orbital Symmetry” – Verlag Chemie, Academic Press, 1970 Pg. 169
11. ^ Zimmerman, H. E., “Five decades of mechanistic and exploratory organic photochemistry”, Pure Appl. Chem., 2006, 78, 2193-2203.