- Mindlin–Reissner plate theory
-
The Mindlin-Reissner theory of plates is an extension of Kirchhoff–Love plate theory that takes into account shear deformations through-the-thickness of a plate. The theory was proposed in 1951 by Raymond Mindlin [1]. A similar, but not identical, theory had been proposed earlier by Eric Reissner in 1945 [2]. Both theories are intended for thick plates in which the normal to the mid-surface remains straight but not necessarily perpendicular to the mid-surface. The Mindlin-Reissner theory is used to calculate the deformations and stresses in a plate whose thickness is of the order of 1/10th the planar dimensions while the Kirchhoff-Love theory is applicable to thinner plates.
The form of Mindlin-Reissner plate theory that is most commonly used is actually due to Mindlin and is more properly called Mindlin plate theory [3]. The Reissner theory is slightly different. Both theories include in-plane shear strains and both are extensions of Kirchhoff-Love plate theory incorporating first-order shear effects.
Mindlin's theory assumes that there is a linear variation of displacement across the plate thickness and but that the plate thickness does not change during deformation. This implies that the normal stress through the thickness is ignored; an assumption which is also called the plane stress condition. On the other hand, Reissner's theory assumes that the bending stress is linear while the shear stress is quadratic through the thickness of the plate. This leads to a situation where the displacement through-the-thickness is not necessarily linear and where the plate thickness may change during deformation. Therefore, Reissner's theory does not invoke the plane stress condition.
The Mindlin-Reissner theory is often called the first-order shear deformation theory of plates. Since a first-order shear deformation theory implies a linear displacement variation through the thickness, it is incompatible with Reissner's plate theory.
Contents
Mindlin theory
Mindlin's theory was originally derived for isotropic plates using equilibrium considerations. A more general version of the theory based on energy considerations is discussed here[4].
Assumed displacement field
The Mindlin hypothesis implies that the displacements in the plate have the form
where x1 and x2 are the Cartesian coordinates on the mid-surface of the undeformed plate and x3 is the coordinate for the thickness direction,
 are the in-plane displacements of the mid-surface, w0 is the displacement of the mid-surface in the x3 direction, φ1 and φ2 designate the angles which the normal to the mid-surface makes with the x3 axis. Unlike Kirchhoff-Love plate theory where φα are directly related to w0, Mindlin's theory requires that
are the in-plane displacements of the mid-surface, w0 is the displacement of the mid-surface in the x3 direction, φ1 and φ2 designate the angles which the normal to the mid-surface makes with the x3 axis. Unlike Kirchhoff-Love plate theory where φα are directly related to w0, Mindlin's theory requires that  and
and  .
.Strain-displacement relations
Depending on the amount of rotation of the plate normals two different approximations for the strains can be derived from the basic kinematic assumptions.
For small strains and small rotations the strain-displacement relations for Mindlin-Reissner plates are
The shear strain, and hence the shear stress, across the thickness of the plate is not neglected in this theory. However, the shear strain is constant across the thickness of the plate. This cannot be accurate since the shear stress is known to be parabolic even for simple plate geometries. To account for the inaccuracy in the shear strain, a shear correction factor (κ) is applied so that the correct amount of internal energy is predicted by the theory. Then
Equilibrium equations
The equilibrium equations of a Mindlin-Reissner plate for small strains and small rotations have the form
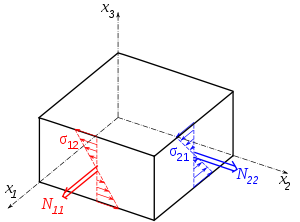
where q is an applied out-of-plane load, the in-plane stress resultants are defined as
the moment resultants are defined as
and the shear resultants are defined as
-
Derivation of equilibrium equations For the situation where the strains and rotations of the plate are small the virtual internal energy is given by
where the stress resultants and stress moment resultants are defined in a way similar to that for Kirchhoff plates. The shear resultant is defined as
Integration by parts gives
The symmetry of the stress tensor implies that Nαβ = Nβα and Mαβ = Mβα. Hence,
For the special case when the top surface of the plate is loaded by a force per unit area
 , the virtual work done by the external forces is
, the virtual work done by the external forces isThen, from the principle of virtual work,
Using standard arguments from the calculus of variations, the equilibrium equations for a Mindlin-Reissner plate are
Boundary conditions
The boundary conditions are indicated by the boundary terms in the principle of virtual work.
If the only external force is a vertical force on the top surface of the plate, the boundary conditions are
Stress-strain relations
The stress-strain relations for a linear elastic Mindlin-Reissner plate are given by
Since σ33 does not appear in the equilibrium equations it is implicitly assumed that it do not have any effect on the momentum balance and is neglected. This assumption is also called the plane stress assumption. The remaining stress-strain relations for an orthotropic material, in matrix form, can be written as
Then,
and
For the shear terms
The extensional stiffnesses are the quantities
The bending stiffnesses are the quantities
Mindlin theory for isotropic plates
For uniformly thick, homogeneous, and isotropic plates, the stress-strain relations in the plane of the plate are
where E is the Young's modulus, ν is the Poisson's ratio, and εαβ are the in-plane strains. The through-the-thickness shear stresses and strains are related by
where G = E / (2(1 + ν)) is the shear modulus.
Constitutive relations
The relations between the stress resultants and the generalized deformations are,
and
The bending rigidity is defined as the quantity
For a plate of thickness h, the bending rigidity has the form
Governing equations
If we ignore the in-plane extension of the plate, the governing equations are
In terms of the generalized deformations, these equations can be written as
-
Derivation of equilibrium equations in terms of deformations If we expand out the governing equations of a Mindlin plate, we have
Recalling that
and combining the three governing equations, we have
If we define
we can write the above equation as
Similarly, using the relationships between the shear force resultants and the deformations, and the equation for the balance of shear force resultants, we can show that
Since there are three unknowns in the problem, φ1, φ2, and w0, we need a third equation which can be found by differentiating the expressions for the shear force resultants and the governing equations in terms of the moment resultants, and equating these. The resulting equation has the form
Therefore, the three governing equations in terms of the deformations are
The boundary conditions along the edges of a rectangular plate are
Relationship to Reissner theory
The canonical constitutive relations for shear deformation theories of isotropic plates can be expressed as[5][6]
Note that the plate thickness is h (and not 2h) in the above equations and D = Eh3 / [12(1 − ν2)]. If we define a Marcus moment,
we can express the shear resultants as
These relations and the governing equations of equilibrium, when combined, lead to the following canonical equilibrium equations in terms of the generalized displacements.
where
In Mindlin's theory, w0 is the transverse displacement of the mid-surface of the plate and the quantities φ1 and φ2 are the rotations of the mid-surface normal about the x2 and x1-axes, respectively. The canonical parameters for this theory are
 and
and  . The shear correction factor κ usually has the value 5 / 6.
. The shear correction factor κ usually has the value 5 / 6.On the other hand, in Reissner's theory, w0 is the weighted average transverse deflection while φ1 and φ2 are equivalent rotations which are not identical to those in Mindlin's theory. The canonical parameters for Reissner's theory are
 ,
,  , and κ = 5 / 6.
, and κ = 5 / 6.Relationship to Kirchhoff-Love theory
If we define the moment sum for Kirchhoff-Love theory as
we can show that [5]
where Φ is a biharmonic function such that
 . We can also show that, if wK is the displacement predicted for a Kirchhoff-Love plate,
. We can also show that, if wK is the displacement predicted for a Kirchhoff-Love plate,where Ψ is a function that satisfies the Laplace equation,
 . The rotations of the normal are related to the displacements of a Kirchhoff-Love plate by
. The rotations of the normal are related to the displacements of a Kirchhoff-Love plate bywhere
References
- ^ R. D. Mindlin, 1951, Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates, ASME Journal of Applied Mechanics, Vol. 18 pp. 31–38.
- ^ E. Reissner, 1945, The effect of transverse shear deformation on the bending of elastic plates, ASME Journal of Applied Mechanics, Vol. 12, pp. A68-77.
- ^ Wang, C. M., Lim, G. T., Reddy, J. N, Lee, K. H., 2001, Relationships between bending solutions of Reissner and Mindlin plate theories, Engineering Structures, vol. 23, pp. 838-849.
- ^ Reddy, J. N., 1999, Theory and analysis of elastic plates, Taylor and Francis, Philadelphia.
- ^ a b Lim, G. T. and Reddy, J. N., 2003, On canonical bending relationships for plates, International Journal of Solids and Structures, vol. 40, pp. 3039-3067.
- ^ These equations use a slightly different sign convention than the preceding discussion.
See also
- Bending
- Bending of plates
- Infinitesimal strain theory
- Linear elasticity
- Plate theory
- Stress (mechanics)
- Vibration of plates
Categories:
Wikimedia Foundation. 2010.










![\begin{align}
\delta U & = \int_{\Omega^0} \int_{-h}^h \boldsymbol{\sigma}:\delta\boldsymbol{\epsilon}~dx_3~d\Omega
= \int_{\Omega^0} \int_{-h}^h \left[\sigma_{\alpha\beta}~\delta\varepsilon_{\alpha\beta} + 2~\kappa~\sigma_{\alpha 3}~\delta\varepsilon_{\alpha 3}\right]~dx_3~d\Omega \\
& = \int_{\Omega^0} \int_{-h}^h \left[\frac{1}{2}~\sigma_{\alpha\beta}~(\delta u^0_{\alpha,\beta}+\delta u^0_{\beta,\alpha}) - \frac{x_3}{2}~\sigma_{\alpha\beta}~(\delta \varphi_{\alpha,\beta}+\delta\varphi_{\beta,\alpha}) + \kappa~\sigma_{\alpha 3}\left(\delta w^0_{,\alpha} - \delta \varphi_\alpha\right)\right]~dx_3~d\Omega \\
& = \int_{\Omega^0} \left[\frac{1}{2}~N_{\alpha\beta}~(\delta u^0_{\alpha,\beta}+\delta u^0_{\beta,\alpha}) - \frac{1}{2}M_{\alpha\beta}~(\delta \varphi_{\alpha,\beta}+\delta\varphi_{\beta,\alpha}) + Q_\alpha\left(\delta w^0_{,\alpha} - \delta \varphi_\alpha\right)\right]~d\Omega
\end{align}](6/2a653d763052d8b573cabc8175f9d9f9.png)

![\begin{align}
\delta U & = \int_{\Omega^0} \left[-\frac{1}{2}~(N_{\alpha\beta,\beta}~\delta u^0_{\alpha}+N_{\alpha\beta,\alpha}~\delta u^0_{\beta})
+ \frac{1}{2}(M_{\alpha\beta,\beta}~\delta \varphi_{\alpha}+M_{\alpha\beta,\alpha}\delta\varphi_{\beta}) - Q_{\alpha,\alpha}~\delta w^0 - Q_\alpha~\delta\varphi_\alpha\right]~d\Omega \\
& + \int_{\Gamma^0} \left[\frac{1}{2}~(n_\beta~N_{\alpha\beta}~\delta u^0_\alpha+n_\alpha~N_{\alpha\beta}~\delta u^0_{\beta})
- \frac{1}{2}(n_\beta~M_{\alpha\beta}~\delta \varphi_{\alpha}+n_\alpha M_{\alpha\beta}\delta\varphi_\beta) + n_\alpha~Q_\alpha~\delta w^0\right]~d\Gamma
\end{align}](0/ff07490bfc93893c3c5ba53d4f5ffe92.png)
![\begin{align}
\delta U & = \int_{\Omega^0} \left[-N_{\alpha\beta,\alpha}~\delta u^0_{\beta}
+ \left(M_{\alpha\beta,\beta}-Q_\alpha\right)~\delta \varphi_{\alpha} - Q_{\alpha,\alpha}~\delta w^0\right]~d\Omega \\
& + \int_{\Gamma^0} \left[n_\alpha~N_{\alpha\beta}~\delta u^0_{\beta}
- n_\beta~M_{\alpha\beta}~\delta \varphi_{\alpha} + n_\alpha~Q_\alpha~\delta w^0\right]~d\Gamma
\end{align}](4/cb40c47ae57fe39efa48a2823c9e65e1.png)

![\begin{align}
& \int_{\Omega^0} \left[N_{\alpha\beta,\alpha}~\delta u^0_{\beta}
- \left(M_{\alpha\beta,\beta}-Q_\alpha\right)~\delta \varphi_{\alpha} + \left(Q_{\alpha,\alpha}+q\right)~\delta w^0 \right]~d\Omega \\
& \qquad \qquad = \int_{\Gamma^0} \left[n_\alpha~N_{\alpha\beta}~\delta u^0_{\beta}
- n_\beta~M_{\alpha\beta}~\delta \varphi_{\alpha} + n_\alpha~Q_\alpha~\delta w^0\right]~d\Gamma
\end{align}](7/7b75aef486ac55cbd550115513acfc85.png)



























![\begin{align}
M_{11} & = D\left[\mathcal{A}\left(\frac{\partial \varphi_1}{\partial x_1}+\nu\frac{\partial \varphi_2}{\partial x_2}\right)
- (1-\mathcal{A})\left(\frac{\partial^2 w^0}{\partial x_1^2} + \nu\frac{\partial^2 w^0}{\partial x_2^2}\right)\right]
+ \frac{q}{1-\nu}\,\mathcal{B}\\
M_{22} & = D\left[\mathcal{A}\left(\frac{\partial \varphi_2}{\partial x_2}+\nu\frac{\partial \varphi_1}{\partial x_1}\right)
- (1-\mathcal{A})\left(\frac{\partial^2 w^0}{\partial x_2^2} + \nu\frac{\partial^2 w^0}{\partial x_1^2}\right)\right]
+ \frac{q}{1-\nu}\,\mathcal{B}\\
M_{12} & = \frac{D(1-\nu)}{2}\left[\mathcal{A}\left(\frac{\partial \varphi_1}{\partial x_2}+\frac{\partial \varphi_2}{\partial x_1}\right)
- 2(1-\mathcal{A})\,\frac{\partial^2 w^0}{\partial x_1 \partial x_2}\right] \\
Q_1 & = \mathcal{A} \kappa G h\left(\varphi_1 + \frac{\partial w^0}{\partial x_1}\right) \\
Q_2 & = \mathcal{A} \kappa G h\left(\varphi_2 + \frac{\partial w^0}{\partial x_2}\right) \,.
\end{align}](5/e8537782591d1665c9813778ac5b8462.png)
![\mathcal{M} = D\left[\mathcal{A}\left(\frac{\partial \varphi_1}{\partial x_1} + \frac{\partial \varphi_2}{\partial x_2}\right)
- (1-\mathcal{A})\nabla^2 w^0\right] + \frac{2q}{1-\nu^2}\mathcal{B}](e/e3ece03c12259aa39b6ba9a339c98971.png)
![\begin{align}
Q_1 & = \frac{\partial \mathcal{M}}{\partial x_1}
+ \frac{D(1-\nu)}{2}\left[\mathcal{A}\frac{\partial }{\partial x_2}\left(\frac{\partial \varphi_1}{\partial x_2}
-\frac{\partial \varphi_2}{\partial x_1}\right)\right] - \frac{\mathcal{B}}{1+\nu}\frac{\partial q}{\partial x_1} \\
Q_2 & = \frac{\partial \mathcal{M}}{\partial x_2}
- \frac{D(1-\nu)}{2}\left[\mathcal{A}\frac{\partial }{\partial x_1}\left(\frac{\partial \varphi_1}{\partial x_2}
-\frac{\partial \varphi_2}{\partial x_1}\right)\right] - \frac{\mathcal{B}}{1+\nu}\frac{\partial q}{\partial x_2}\,.
\end{align}](c/acc3cce823fae9ce779cc8075988f5b6.png)






