Maurer rose

In geometry, the concept of a Maurer rose was introduced by Peter M. Maurer in his article titled A Rose is a Rose...[1]. A Maurer rose consists of some lines that connect some points on a rose curve.

A Maurer rose with n = 7 and d = 29

Definition

Let r = sin(nθ) be a rose in the polar coordinate system, where n is a positive integer. The rose has n petals if n is odd, and 2n petals if n is even.

We then take 361 points on the rose:

(sin(nk), k) (k = 0, d, 2d, 3d, ..., 360d),

where d is a positive integer and the angles are in degrees, not radians.

A Maurer rose of the rose r = sin(nθ) consists of the 360 lines successively connecting the above 361 points. Thus a Maurer rose is a polygonal curve with vertices on a rose.

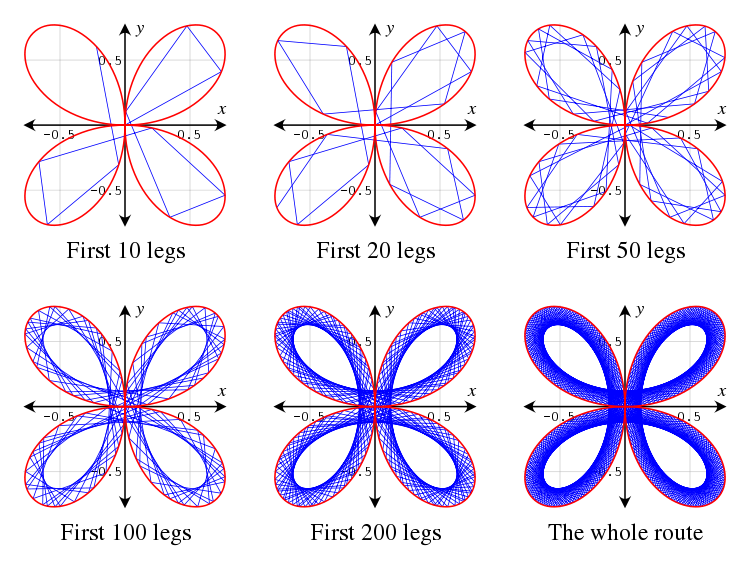
A Maurer rose can be described as a closed route in the polar plane. A walker starts a journey from the origin, (0, 0), and walks along a line to the point (sin(nd), d). Then, in the second leg of the journey, the walker walks along a line to the next point, (sin(n·2d), 2d), and so on. Finally, in the final leg of the journey, the walker walks along a line, from (sin(n·359d), 359d) to the ending point, (sin(n·360d), 360d). The whole route is the Maurer rose of the rose r = sin(nθ). A Maurer rose is a closed curve since the starting point, (0, 0) and the ending point, (sin(n·360d), 360d), coincide.

The following figure shows the evolution of a Maurer rose (n = 2, d = 29° ).

Images

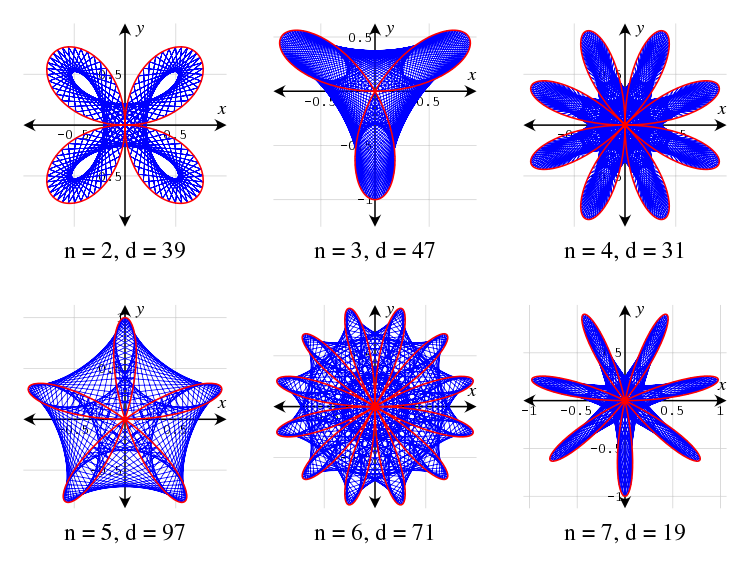
The following are some Maurer roses drawn with some values for n and d:

Maple code

Below is the Maple code for plotting Maurer roses (different values of n and d can be chosen by the user):

with(plots)  :
n:=7:d:=29:
Rose:=plot(sin(n*t),t=0..2*Pi,coords=polar,thickness=2):
K:=360:
for k from 0 to K do k1:=k*d*Pi/180:k2:=(k+1)*d*Pi/180:
Point[k]:=pointplot([sin(n*k1),k1],coords=polar,color=blue):
Maurer_rose[k]:=listplot([[sin(n*k1),k1],[sin(n*k2),k2]],coords=polar,color=blue):od:
Maurer_rose:=display(seq(Maurer_rose[k],k=0..K)):
Point:=display(seq(Point[k],k=0..K)):
display(Rose,Point,Maurer_rose);

References

• Maurer, Peter M. (August-September 1987). "A Rose is a Rose...". The American Mathematical Monthly 94 (7): 631–645. doi:10.2307/2322215. JSTOR 2322215. http://www.toodoc.com/Peter-M.-Maurer-ebook.html. 
• Weisstein, Eric W. "Interactive Demonstrations of Maurer roses". MathWorld. Wolfram.com. http://mathworld.wolfram.com/MaurerRose.html.