Dimensionless momentum-depth relationship in open-channel flow

Momentum in Open Channel Flow

What is Momentum?

Momentum for one-dimensional flow in a channel can be given by the expression:

$M=\frac{Q^2}{gA}+\overline yA$

where: M is the momentum [ft3] Q is the rate of flow [ft3/s] g is the acceleration due to gravity [32.2 ft/s2] A is the cross sectional area of flow [ft2] ȳ is the distance from the centroid of A to the water surface [ft]

For Open Channel Flow Calculations where momentum can be assumed to be conserved, we can equate the Momentum at an upstream location, M₁, to that at a downstream location, M₂, such that:

$M_1=M_2=\frac{Q^2}{gA_1}+\overline y_1A_1=\frac{Q^2}{gA_2}+\overline y_2A_2$

Momentum in a Rectangular Channel

In the unique circumstance where the flow is in a rectangular channel (such as a laboratory flume), we can describe this relationship as Unit Momentum, by dividing both sides of the equation by the width of the channel. This produces _uM in terms of ft², and is given by the equation:

${_uM_1}={_uM_2}=\frac{q^2}{gy_1}+ \frac{y_1^2}{2} =\frac{q^2}{gy_2}+ \frac{y_2^2}{2}$

where: uM is M/b q is Q/b b is the base width of the rectangular channel [ft]

Why is Momentum Important?

Momentum allows us to describe the characteristics of flow when energy is not conserved. HEC-RAS, a widely used computer model developed by the US Army Corps of Engineers for calculating water surface profiles, considers that any time flow passes through critical depth, the basic assumption of gradually varied flow required for the Energy Equation to be not applicable. Locations where flow may make such a transition include: significant changes in slope, channel geometry (e.g. bridge sections), grade control structures, and the confluence of water bodies. In these instances, HEC-RAS will use a form of the momentum equation to solve for the water surface elevation at an unknown location.

What are the characteristics of Momentum?

For discussion, we will consider an ideal, frictionless, rectangular channel. For each value of q, a unique curve can be produced where M is shown as a function of depth. As is the case for specific energy, the minimum value of _uM, _uM_min, corresponds to critical depth. For each value of _uM greater than _uM_min, there are two depths that can occur. These are called conjugate depths, and represent supercritical and subcritical alternatives for flow of a given _uM. Since hydraulic jumps conserve momentum, if the depth at the upstream or downstream end of a hydraulic jump is known, we can determine the unknown depth by drawing a vertical line through the known depth and reading its conjugate.

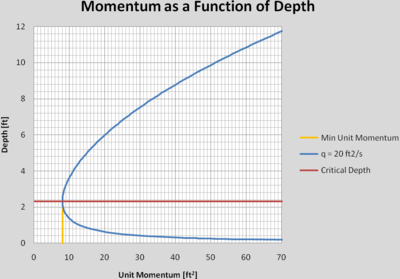
Dimensionless M’-y’ diagram

Why do we need a Dimensionless Momentum-Depth Relationship?

Conjugate depths can be determined from curves like the one above. However, since this curve is unique for q = 20 ft²/s, we would have to develop a new curve for each rectangular channel of a given base width (or discharge). If we can establish a dimensionless relationship, we can apply the curve to any problem in which the cross-section is rectangular in shape. To create a dimensionless Momentum-Depth relationship, we will divide both sides by a normalizing value that will allow us to use a dimensionless relationship between Momentum and Depth for all values of q.

Derivation of the Dimensionless Momentum-Depth Relationship

Given that:

${_uM_1}={_uM_2}=\frac{q^2}{gy_1}+ \frac{y_1^2}{2} =\frac{q^2}{gy_2}+ \frac{y_2^2}{2}$

and that:

${q^2}={gy_c^2}$

we can normalize the relationship between depth and Momentum by dividing both by the value of critical depth squared and substituting for q² to yield:

$\frac{_uM}{y_c^2} = \frac{gy_c^3}{gyy_c^2} + \frac{y^2}{2y_c^2}$

where: yc is the critical depth.

If we let M’ = _uM/y_c², and y’ = y/y_c, this equation becomes:

$M'= \frac{1}{y'} + \frac{y'^2}{2}$

The Dimensionless Momentum-Depth diagram

By applying the conversion to dimensionless units described above, the Dimensionless Momentum-Depth diagram is produced below.

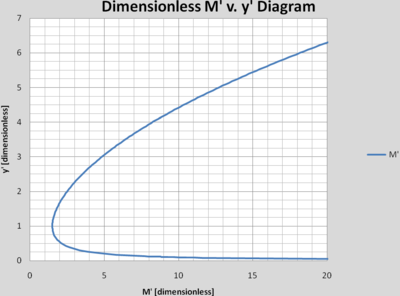
What is the relationship between the Dimensionless Momentum-Depth Diagram and the Dimensionless Energy-Depth Diagram?

By close inspection of the Dimensionless Energy-Depth Diagram, an interesting conclusion can be drawn, which is that M’ is the same function of y’ as E’ is of 1/y’, and vice versa. This is demonstrated in the following chart that compares favorably to the chart of the Dimensionless Energy-Depth Diagram. Note that the only difference between the chart above and the one below is the values of the y-axis are the reciprocal of one another and that the scale has been changed to be consistent with the scale found in the discussion of Dimensionless Energy-Depth.

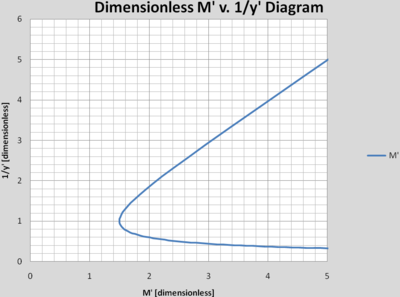
Because Energy and Momentum have this reciprocal relationship (found also in the non-dimensionless forms of these relationships), we can use a Dimensionless Energy-Depth Diagram to create a Dimensionless Momentum-Depth Diagram, and vice versa.

Solution of simple version of hydraulic jump with dimensionless diagram

To demonstrate the use of a Dimensionless Momentum-Depth Diagram in the solution of a simple hydraulic jump problem, let’s consider a rectangular channel with a base width of 10 ft, and a flow rate of 100 ft³/s, with a tailwater induced downstream depth of 6 ft. What is the depth of flow at the upstream end of the hydraulic jump?

Step 1 – Calculate q:

$q=\frac{Q}{b}$

$q=\frac{100 ft^3/s}{10 ft}=10ft^2/s$

Step 2 – Calculate y_c:

$y_c=\sqrt[3]{q^2 \over g}$

$y_c=\sqrt[3]{{(10 ft^2/s)}^2 \over 32.2 ft/s^2}=1.459 ft$

(note-calculations are displayed to 3 decimal places to reduce rounding errors in Step 6)

Step 3 – Calculate y’ for the downstream depth:

$y'=\frac{y_d}{y_c}$

$y'=\frac{6 ft}{1.46 ft}=4.112$

Step 4 – Determine Conjugate Dimensionless Depth from Chart:

Using the Dimensionless Chart presented above, plot y’ = 4.11 over to its intersection with the M’ curve. Read down the chart to find the conjugate depth and determine the new y’ from the left axis.

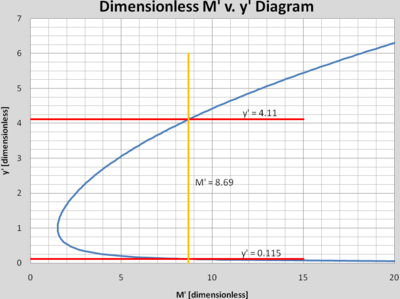
Step 5 – Calculate the upstream (conjugate) depth to 6 ft by converting y’ = 0.115 to its actual depth:

$y'=\frac{y_u}{y_c}$

yu = y'yc = 0.115(1.459ft) = 0.168ft

Step 6 – Validation:

${_uM_u}=\frac{q^2}{gy_1}+ \frac{y_1^2}{2}$

${_uM_u}=\frac{10^2}{(32.2)0.168}+ \frac{0.168^2}{2}=18.500ft^2$

and

${_uM_d}=\frac{q^2}{gy_2}+ \frac{y_2^2}{2}$

${_uM_d}=\frac{10^2}{(32.2)6}+ \frac{6^2}{2}=18.518ft^2$

The difference between _uM_u and _uM_d is shown as 0.18 ft² due to rounding errors. Therefore, _uM_u and _uM_d are shown to represent the same unit momentum across the jump and momentum is conserved, validating the calculations using the Dimensionless Chart above.

This topic contribution was made in partial fulfillment of the requirements for Virginia Tech, Department of Civil and Environmental Engineering course: CEE 5984 – Open Channel Flow during the Fall 2010 semester.

References

• Brunner, G.W., HEC-RAS, River Analysis System Hydraulic Reference Manual (CPD-69), US Army Corps of Engineers, Hydrologic Engineering Center, 2010.
• Chaudhry, M.H., Open-Channel Flow (second edition), Springer Science+Business Media, llc, 2008.
• French, R.H., Open-Channel Hydraulics, McGraw-Hill, Inc., 1985.
• Henderson, F.M., Open Channel Flow, Prentice-Hall, 1966.
• Janna, W.S., Introduction to Fluid Mechanics, PWS-Kent Publishing Company, 1993.
• Linsey, R.K., Franzini, J.B., Freyberg, D.L., Tchobanoglous, G., Water-Resources Engineering (fourth edition), McGraw-Hill, Inc., 1992.