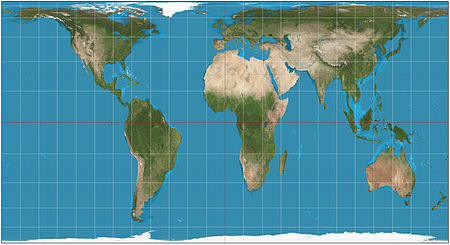
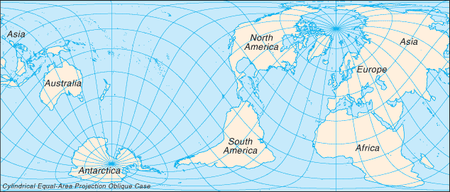
Cylindrical equal-area projection

Cylindrical equal-area projection of the world; standard parallel at 40°N.

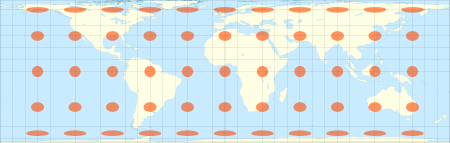The Lambert cylindrical equal-area projection with Tissot's indicatrix of deformation

Cylindrical equal-area projection with oblique orientation

In cartography, the cylindrical equal-area projection is a family of cylindrical, equal area map projections.

Cylindrical projections

Main article: Cylindrical map projection

The term "normal cylindrical projection" is used to refer to any projection in which meridians are mapped to equally spaced vertical lines and circles of latitude (parallels) are mapped to horizontal lines (or, mutatis mutandis, more generally, radial lines from a fixed point are mapped to equally spaced parallel lines and concentric circles around it are mapped to perpendicular lines).

The mapping of meridians to vertical lines can be visualized by imagining a cylinder (of which the axis coincides with the Earth's axis of rotation) wrapped around the Earth and then projecting onto the cylinder, and subsequently unfolding the cylinder.

By the geometry of their construction, cylindrical projections stretch distances east-west. The amount of stretch is the same at any chosen latitude on all cylindrical projections, and is given by the secant of the latitude as a multiple of the equator's scale. The various cylindrical projections are distinguished from each other solely by their north-south stretching (where latitude is given by φ):

The only cylindrical projections that preserve area have a

• North-south compression precisely the reciprocal of east-west stretching (cosine φ): equal-area cylindrical (with many named specializations such as Gall–Peters or Gall orthographic, Behrmann, and Lambert cylindrical equal-area). This divides north-south distances by a factor equal to the secant of the latitude, preserving area but heavily distorting shapes.

Any particular cylindrical equal-area map has a pair of identical latitudes of opposite sign (or else the equator) at which the east-west scale matches the north-south-scale.

Description

Formulae

All cylindrical equal-area projections use the formula:

$x = ( \lambda - \lambda_0 ) \cos \phi_0\,$

$y = \sin \phi / \cos \phi_0\,$

where $\lambda\,$ is the longitude, $\lambda_0\,$ is the central meridian, $\phi\,$ is the latitude, and $\phi_0\,$ is the standard latitude^[1], all expressed in radians.

Some cartographers prefer to work in degrees, rather than radians, and use the equivalent formula:

$x = ( \lambda - \lambda_0 ) (\cos \phi_0) \pi / 180^\circ$

$y = \sin \phi / \cos \phi_0\,$

Simplified formula

Stripping out unit conversion and uniform scaling, the formulae may be written:

$x = ( \lambda - \lambda_0 ) S\,$

$y = \sin\phi\,$

Hence the sphere is mapped onto a stretched vertical cylinder. The stretch factor S is what distinguishes the variations of cylindric equal-area projection.

Discussion

The various specializations of the cylindric equal-area projection differ only in the ratio of the vertical to horizontal axis. This ratio determines the standard parallel of the projection, which is the parallel at which there is no distortion and along which distances match the stated scale. There are always two standard parallels on the cylindric equal-area projection, each at the same distance north and south of the equator. The standard parallels of the Gall–Peters are 45° N and 45° S. Several other specializations of the equal-area cylindric have been described, promoted, or otherwise named.^[2][3][4][5]

Named specializations of the cylindrical equal-area projection

Projection	Image	Creator (year)	Standard parallels N/S	Width/height aspect ratio	Notes
cylindrical equal-area			$\phi_0\,$	$\pi(\cos \phi_0)^2\,$	Base projection for all the others.
Lambert		Johann Heinrich Lambert (1772)	Equator (0°)	$\pi \approx 3.14$
Behrmann		Walter Behrmann (1910)	30°	$3\pi/4 \approx 2.36 \approx$ δS
Smyth equal-surface = Craster rectangular		C. Piazzi Smyth (1870)	37°04'	2.0
Trystan Edwards		Trystan Edwards (1953)	37°24'	$\approx 2.0$
Hobo–Dyer		Mick Dyer (2002)	37°30'	$\approx 2.0$
Gall–Peters = Gall orthographic = Peters		James Gall (1855)	45°	$\pi/2 \approx 1.6 \approx$ Φ	Promoted by Arno Peters as a new invention in 1967.
Balthasart		M. Balthasart (1935)	50°	$\approx 1.3$

History

The invention of the Lambert cylindrical equal-area projection is attributed to the Alsatian mathematician Johann Heinrich Lambert in 1772.^[6]

Arno Peters devised an equal-area map in 1967 and presented it as a "new invention in 1973."

The Tobler hyperelliptical projection, first described by Tobler in 1973, is a further generalization of the cylindrical equal-area family.

The HEALPix projection is an equal-area hybrid combination of: the Lambert cylindrical equal-area projection, for the equatorial regions of the sphere; and an interrupted Collignon projection, for the polar regions.

See also

• Lambert azimuthal equal-area projection
• Lambert conformal conic projection

References

1. ^ Map Projections - A Working Manual, USGS Professional Paper 1395, John P. Snyder, 1987, pp.76–85
2. ^ Snyder, John P. (1989). An Album of Map Projections p. 19. Washington, D.C.: U.S. Geological Survey Professional Paper 1453. (Mathematical properties of the Gall–Peters and related projections.)
3. ^ Monmonier, Mark (2004). Rhumb Lines and Map Wars: A Social History of the Mercator Projection p. 152. Chicago: The University of Chicago Press. (Thorough treatment of the social history of the Mercator projection and Gall–Peters projections.)
4. ^ Smyth, C. Piazzi. (1870). On an Equal-Surface Projection and its Anthropological Applications. Edinburgh: Edmonton & Douglas. (Monograph describing an equal-area cylindric projection and its virtues, specifically disparaging Mercator's projection.)
5. ^ Weisstein, Eric W. "Cylindrical Equal-Area Projection." From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/CylindricalEqual-AreaProjection.html
6. ^ Mulcahy, Karen. "Cylindrical Projections". City University of New York. http://www.geo.hunter.cuny.edu/mp/cylind.html. Retrieved 2007-03-30. 

External links

• Table of examples and properties of all common projections, from radicalcartography.net
• An interactive Java Applet to study the metric deformations of the Lambert Cylindrical Equal-Area Projection.