Closure problem

A Closure problem is a problem in graph theory for finding a set of vertices in a directed graph such that there are no edges from the set to the rest of the graph. More specifically, the minimum closure problem asks for a set of this type with the minimum possible weight in a weighted graph.

Closure problem

Definition

In a directed graph G = (V, A), a set S of vertices is said to be closed if every successor of every vertex S is also in S. Equivalently, S is closed if it has no outgoing edge.

It may be assumed without loss of generality that G is a directed acyclic graph. For, if it is not acyclic, each of its strongly connected components must either be entirely contained in or entirely disjoint from any closed set. Therefore, the closures of G are in one-to-one correspondence with the closures of the condensation of G, a directed acyclic graph that has one vertex for each strongly connected component of G. In weighted closure problems, one may set the weight of any vertex of the condensation to the sum of the weights of the vertices in the corresponding strongly connected component of G.

Minimum closure problem

For a directed graph G = (V, A) with vertex weights w_i the minimum closure problem is to find a closed set of total minimum weight. If all the weights are positive or negative, the minimum closure problem is trivial. Indeed, if all weights are positive the empty subgraph is a solution, and if all weights are negative, the whole graph is solution. We may therefore assume that G has both positive and negative weights.

Open-pit mining

Picard studied the closure problem on the open-pit mining problem, which he modeled as a maximym-closure problem.

Maximum and minimum closure problem

Setting up the graph for a closure problem

In the maximum closure problem a directed graph G = (V, A) with vertex weights w_i is given and we want to find a closed subset of vertices V ' such that $\sum_{i \in V'} w_i$ is maximum. Picard showed that the maximum closure problem can be solved using a minimum cut procedure. Additionally it is clear that the selection problem is closure problem on a bipartite graph therefore the selection problem is a special case of the closure problem. Maximum and minimum closure problems can be converted to each other by negating the vertex weights. A maximum closure problem can be formulated as follows

$\max \sum_{j \in V} w_jx_j$

$\mbox{subject to}\; x_j\leq x_i \;\;\;\;\forall(i,j)\in A$

$x_j \in \left\{0,1\right\} \;\;\;\;\;\;\;\;\;\; \forall j \in V$

Where x_i is 1 if the vertex is in the closure and it is 0 otherwise, and the first constraint ensures that if a vertex is in the closure its successor is also in it. Since each row has at most one 1 and one −1 we know that the constraint matrix is totally unimodular and an integer solution is obtained by solving the LP relaxation of the problem.

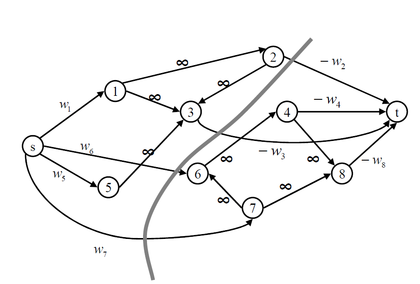
In order to solve the maximum closure problem we can use the max-flow min-cut theorem. Let us construct the s-t graph for maximum closure problem. The graph has a vertex j for each variable x_j. We also add a source s and a sink vertex t. If the weight of the variable w_j is positive we include an arc from the source to the vertex j with capacity w_j. If the weight is negative we add the arc from j to the sink vertex (t) with capacity −w_j. Each inequality x_j ≤ x_i is associated with an arc (i, j) with capacity ∞. Let V⁺be the set of vertices with positive weights and V⁻ the set of vertices with negative weights. Figure \ref{fig:cl4} shows the graph constructed for the closure problem. We can find the minimum cut in this graph by solving a max-flow problem from source to the sink . The source set of a minimum cut separating s from t is a maximum closure in the graph. This statement holds because the minimum cut is finite and cannot include any arc from A that has the weight equal to ∞ [5]. Minimizing the value of the finite cut is equivalent to maximizing the sum of weights of the vertices in the source set of the finite cut. Denote (A,B) the collection of arc with tails at A and heads at B. Also $C\left(A,B\right)=\sum_{i \in A, j \in B} c_{ij}$ where c_ijis the capacity of arc (i,j). Let $w\left(A\right)=\sum_{j \in A}w_j$. For a finite cut $\left(\left\{s\right\}\cup S, \bar{S} \cup \left\{t\right\}\right)$ we have:

$\min_{\bar{S}\subseteq V} [C\left(\{s\}\cup S, \bar{S} \cup \left\{t\right\}\right)] = \min_{\bar{S}\subseteq V} \sum_{j \in \bar{S}\cap V^+} w_j + \sum_{j \in S\cap V^-}\left(-w_j\right)$

$\min_{\bar{S}\subseteq V} \sum_{j \in \bar{S}\cap V^+} w_j - \left(\sum_{i \in V^-}w_j- \sum_{i \in \bar{S}\cap V^-}w_i\right)$

$\min_{\bar{S}\subseteq V} \sum_{j \in \bar{S}} w_j - w\left(V^-\right).$

In the last expression $w\left(V^-\right)$ is a constant. Therefore the closed set $\bar{S}$ of minimum weight is also the sink set of the minimum cut and vice versa—the sink set of a minimum cut (without t), which has to be finite, also minimized the weight of the closure.

History

During the 1970s J.C. Picard was working on the open-pit mining problem and during that time worked on generalizing the selection problem to the closure problem. During that time the mining industry was developing optimization methods on their own. Picard's contribution introduced the closure problem to the mining industry.

References

[1] D. S. Hochbaum. Complexity and algorithms for convex network optimization and other nonlinear problems. 4OR , 3:3, 2005, 171 - 216

[2] D. S. Hochbaum. An efficient algorithm for image segmentation, Markov Random Fields and related problems. Journal of the ACM, Vol 48, No 2, July 2001 pp. 686 – 701.

[3] D. S. Hochbaum. Selection, Provisioning, Shared Fixed Costs, Maximum Closure, and Implications on Algorithmic Methods Today, Management Science, Vol 50:6, pp 709–723, 2004. Link

[4] D. S. Hochbaum. The Pseudo flow algorithm: A new algorithm for the maximum flow problem, Operations Research, Vol 58(4) 992-1009, July-Aug (2008).

[5] D. S. Hochbaum, M. Queyranne. Minimizing a convex cost closure set. Siam Journal on Discrete Mathematics, 16:2, 2003, pp 192–207. Extended abstract appeared in Lecture Notes in Computer Science 1879, M. Paterson (ed.), 8th Annual European Symposium on Algorithms - ESA 2000 proceedings pp 256–267.

[6] D. S. Hochbaum, J. George Shanthikumar. Convex separable optimization is not much harder than linear optimization. Journal of the ACM, Volume 37 , Issue 4, Pages: 843 - 862.