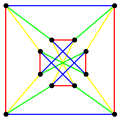
Chvátal graph

Chvátal graph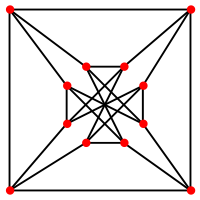
Chvátal graph
Chvatal graph.draw.svg
Named after Václav Chvátal
Vertices 12
Edges 24
Radius 2
Diameter 2
Girth 4
Automorphisms 8 (D4)
Chromatic number 4
Chromatic index 4
Properties Regular
Hamiltonian
Triangle-free
Eulerian
v · mathematical field of graph theory, the Chvátal graph is an undirected graph with 12 vertices and 24 edges, discovered by Václav Chvátal (1970).

It is triangle-free: its girth (the length of its shortest cycle) is four. It is 4-regular: each vertex has exactly four neighbors. And its chromatic number is 4: it can be colored using four colors, but not using only three. It is, as Chvátal observes, the smallest possible 4-chromatic 4-regular triangle-free graph; the only smaller 4-chromatic triangle-free graph is the Grötzsch graph, which has 11 vertices but has maximum degree 5 and is not regular.

By Brooks’ theorem, every k-regular graph (except for odd cycles and cliques) has chromatic number at most k. It was also known since Erdős (1959) that, for every k and l there exist k-chromatic graphs with girth l. In connection with these two results and several examples including the Chvátal graph, Branko Grünbaum (1970) conjectured that for every k and l there exist k-chromatic k-regular graphs with girth l. The Chvátal graph solves the case k = l = 4 of this conjecture. Grünbaum's conjecture was disproven for sufficiently large k by Johannsen (see Reed 1998), who showed that the chromatic number of a triangle-free graph is O(Δ/log Δ) where Δ is the maximum vertex degree and the O introduces big O notation. However, despite this disproof, it remains of interest to find examples such as the Chvátal graph of high-girth k-chromatic k-regular graphs for small values of k.

An alternative conjecture of Bruce Reed (1998) states that high-degree triangle-free graphs must have significantly smaller chromatic number than their degree, and more generally that a graph with maximum degree Δ and maximum clique size ω must have chromatic number

\chi(G)\le\left\lceil\frac{\Delta+\omega+1}{2}\right\rceil.

The case ω = 2 of this conjecture follows, for sufficiently large Δ, from Johanssen's result. The Chvátal graph shows that the rounding up in Reed's conjecture is necessary, because for the Chvátal graph, (Δ + ω + 1)/2 = 7/2, a number that is less than the chromatic number but that becomes equal to the chromatic number when rounded up.

The Chvátal graph is Hamiltonian, and plays a key role in a proof by Fleischner & Sabidussi (2002) that it is NP-complete to determine whether a triangle-free Hamiltonian graph is 3-colorable.

The characteristic polynomial of the Chvátal graph is (x − 4)(x − 1)4x2(x + 1)(x + 3)2(x2 + x − 4). The Tutte polynomial of the Chvátal graph has been computed by Björklund et al. (2008).

Gallery

  • The chromatic number of the Chvátal graph is 4.

  • The chromatic index of the Chvátal graph is 4.

  • The Chvátal graph is Hamiltonian.

  • Alternative drawing of the Chvátal graph.

References

External links


Wikimedia Foundation. 2010.

Look at other dictionaries:

  • Chvátal — Family name Pronunciation Czech pronunciation: [ˈxvaːtal] Region of origin Czech lands Language(s) of origin Czech Related names …   Wikipedia

  • Graph toughness — In graph theory, toughness is a measure of the connectivity of a graph. A graph G is said to be t tough if, for every k > 1, G cannot be split into k different connected components by the removal of fewer than tk vertices. For instance, a graph… …   Wikipedia

  • Václav Chvátal — Václav (Vašek) Chvátal (born 1946 [http://www.ece.tufts.edu/colloquia/archives/fall00/perfectGraphs.html Biography included with abstract for talk by Chvátal at Tufts Univ., 2000] .] ) (pronounced|ˈvaːt͡slaf ˈxvaːtal) is a professor in the… …   Wikipedia

  • Graphe de Chvátal — Le graphe de Chvátal Nombre de sommets 12 Nombre d arêtes 24 Distribution des degrés 4 régulier Rayon 2 …   Wikipédia en Français

  • Hypohamiltonian graph — In the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.HistoryHypohamiltonian graphs were first… …   Wikipedia

  • Hamiltonischer Graph — Das Hamiltonkreisproblem ist ein fundamentales, NP vollständiges Problem der Graphentheorie. Es fragt, ob in einem gegebenen Graph ein sogenannter Hamiltonkreis existiert. Ein Hamiltonkreis ist dabei ein Kreis, der alle Knoten des Graphen enthält …   Deutsch Wikipedia

  • Hamiltonscher Graph — Das Hamiltonkreisproblem ist ein fundamentales, NP vollständiges Problem der Graphentheorie. Es fragt, ob in einem gegebenen Graph ein sogenannter Hamiltonkreis existiert. Ein Hamiltonkreis ist dabei ein Kreis, der alle Knoten des Graphen enthält …   Deutsch Wikipedia

  • Grötzsch graph — infobox graph name = Grötzsch graph namesake = Herbert Grötzsch vertices = 11 edges = 20 chromatic number = 4 chromatic index = girth = 4 properties = The Grötzsch graph is a triangle free graph with 11 vertices, 20 edges, and chromatic number 4 …   Wikipedia

  • Outerplanar graph — A maximal outerplanar graph and its 3 coloring. In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing.… …   Wikipedia

  • Crossing number (graph theory) — A drawing of the Heawood graph with three crossings. This is the minimum number of crossings among all drawings of this graph, so the graph has crossing number cr(G) = 3. In graph theory, the crossing number cr(G) of a graph G is the… …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”