Christensen Failure Criterion

Failure criteria for isotropic materials has been a long standing problem. Despite many historical attempts, there have not been any successful general forms that span the range from ductile to brittle materials. A new failure criterion that aims to do so has been recently developed. The isotropic material failure theory by Christensen^[1] has a two property form calibrated by the uniaxial tensile and compressive strengths T $\left (\sigma_T\right )$ and C $\left (\sigma_C\right )$. It is based upon a sequence of seven related archive journal papers, the first of which was published in 1997^[2][3]. The website describing it in considerable detail was started in 2007, and it was first utilized by eFunda^[4] in 2008.

The overall failure criterion is composed of two separate subcriteria representing competitive failure mechanisms. when expressed in principal stress components, it is given by :

Polynomial Invariants Failure Criterion

For $0\le\frac{T}{C}\le1$

$\left (\frac{1}{T}-\frac{1}{C} \right )\left (\sigma_1+\sigma_2+\sigma_3\right )+\frac{1}{2TC}\left [\left (\sigma_1-\sigma_2\right )^2+\left (\sigma_2-\sigma_3\right )^2+\left (\sigma_3-\sigma_1\right )^2\right ]\le 1$

(1)

Coordinated Fracture Criterion

For $0\le \frac{T}{C}\le \frac{1}{2}$

$\begin{array}{lcl} \sigma_1 & \le & T \\ \sigma_2 & \le & T \\ \sigma_3 & \le & T \end{array}$

(2)

For plane stresses,σ₃ = 0 and T/C=0.3(brittle materials). Blue line is polynomial invariants failure criterion (1). Red line is coordinated fracture criterion(2).

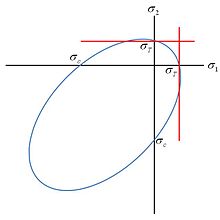
The geometric form of (1) is that of a paraboloid in principal stress space. The fracture criterion (2) (applicable only over the partial range 0 ≤ T/C ≤ 1/2 ) cuts slices off the paraboloid, leaving three flattened elliptical surfaces on it. The fracture cutoff is vanishingly small at T/C=1/2 but it grows progressively larger as T/C diminishes.

The organizing principle underlying the theory is that all isotropic materials admit a distinct classification system based upon their T/C ratio. The comprehensive failure criterion (1) and (2) reduces to the Mises criterion at the ductile limit, T/C = 1. At the brittle limit, T/C = 0, it reduces to a form that cannot sustain any tensile components of stress.

Many cases of verification have been examined over the complete range of materials from extremely ductile to extremely brittle types^[1]. Also, examples of applications have been given. Related criteria distinguishing ductile from brittle failure behaviors have been derived and interpreted.

Applications have been given by Ha^[5] to the failure of the isotropic, polymeric matrix phase in fiber composite materials.

References

1. ^ ^{a b} Christensen, R. M.,(2010),http://www.failurecriteria.com.
2. ^ Christensen, R.M. (1997).Yield Functions/Failure Criteria for Isotropic Materials, Pro. Royal Soc. London, Vol. 453, No. 1962, pp. 1473-1491
3. ^ Christensen, R.M. (2007), A Comprehensive Theory of Yielding and Failure for Isotropic Materials, J. Engr. Mater. and Technol., 129, 173-181
4. ^ eFunda,(2010),http://www.efunda.com/home.cfm.
5. ^ S. K. Ha, K. K. Jin and Y. C. Huang,(2008), Micro-Mechanics of Failure (MMF) for Continuous Fiber Reinforced Composites. Journal of Composite Materials, vol. 42, no. 18, pp. 1873-1895.

See also

• Strength of materials
• Failure theory (material)
• Von Mises yield criterion
• Mohr–Coulomb theory