Orthogonality principle

In statistics and signal processing, the orthogonality principle is a necessary and sufficient condition for the optimality of a Bayesian estimator. Loosely stated, the orthogonality principle says that the error vector of the optimal estimator (in a mean square error sense) is orthogonal to any possible estimator. The orthogonality principle is most commonly stated for linear estimators, but more general formulations are possible. Since the principle is a necessary and sufficient condition for optimality, it can be used to find the minimum mean square error estimator.

Orthogonality principle for linear estimators

The orthogonality principle is most commonly used in the setting of linear estimation.^[1] In this context, let x be an unknown random vector which is to be estimated based on the observation vector y. One wishes to construct a linear estimator $\hat{x} = Hy + c$ for some matrix H and vector c. Then, the orthogonality principle states that an estimator $\hat{x}$ achieves minimum mean square error if and only if

• $E \{ (\hat{x} - x ) y^T \} = 0,$ and
• $E \{ \hat{x} - x \} = 0.$

If x and y have zero mean, then it suffices to require the first condition.

Example

Suppose x is a Gaussian random variable with mean m and variance $\sigma_x^2.$ Also suppose we observe a value y = x + w, where w is Gaussian noise which is independent of x and has mean 0 and variance $\sigma_w^2.$ We wish to find a linear estimator $\hat{x} = hy+c$ minimizing the MSE. Substituting the expression $\hat{x} = hy + c$ into the two requirements of the orthogonality principle, we obtain

• $0 = E \{ (\hat{x} - x ) y \} = E \{ (hx+hw+c-x)(x+w) \} = h (\sigma_x^2+m^2) + h \sigma_w^2 + cm - (\sigma_x^2+m^2) .$
• $0 = E \{ \hat{x} - x \} = E \{ hx+hw+c-x \} = (h-1)m + c .$

Solving these two linear equations for h and c results in

$h = \frac{\sigma_x^2}{\sigma_x^2+\sigma_w^2}, \quad c = \frac{\sigma_w^2}{\sigma_x^2 + \sigma_w^2} m ,$

so that the linear minimum mean square error estimator is given by

$\hat{x} = \frac{\sigma_x^2}{\sigma_w^2 + \sigma_x^2} y + \frac{\sigma_w^2}{\sigma_x^2+\sigma_w^2} m.$

This estimator can be interpreted as a weighted average between the noisy measurements y and the prior expected value m. If the noise variance $\sigma_w^2$ is low compared with the variance of the prior $\sigma_x^2$ (corresponding to a high SNR), then most of the weight is given to the measurements y, which are deemed more reliable than the prior information. Conversely, if the noise variance is high relative to the prior variance, then the estimate will be close to m, as the measurements are not reliable enough to outweigh the prior information.

Finally, note that because the variables x and y are jointly Gaussian, the minimum MSE estimator is linear.^[2] Therefore, in this case, the estimator above minimizes the MSE among all estimators, not only linear estimators.

General formulation

Let V be a Hilbert space of random variables with an inner product defined by $\langle x,y \rangle = E \{ x^H y \}$. Suppose W is a closed subspace of V, representing the space of all possible estimators. One wishes to find a vector $\hat{x} \in W$ which will approximate a vector $x \in V$. More accurately, one would like to minimize the mean squared error (MSE) $E \| x - \hat{x} \|^2$ between $\hat{x}$ and x.

In the special case of linear estimators described above, the space V is the set of all functions of x and y, while W is the set of linear estimators, i.e., linear functions of y only. Other settings which can be formulated in this way include the subspace of causal linear filters and the subspace of all (possibly nonlinear) estimators.

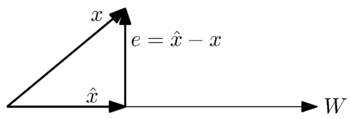
Geometrically, we can see this problem by the following simple case where W is a one-dimensional subspace:

We want to find the closest approximation to the vector x by a vector $\hat{x}$ in the space W. From the geometric interpretation, it is intuitive that the best approximation, or smallest error, occurs when the error vector, e, is orthogonal to vectors in the space W.

More accurately, the general orthogonality principle states the following: Given a closed subspace W of estimators within a Hilbert space V and an element x in V, an element $\hat{x} \in W$ achieves minimum MSE among all elements in W if and only if $E \{ (x-\hat{x}) y^T \} = 0$ for all $y \in W.$

Stated in such a manner, this principle is simply a statement of the Hilbert projection theorem. Nevertheless, the extensive use of this result in signal processing has resulted in the name "orthogonality principle."

A solution to error minimization problems

The following is one way to find the minimum mean square error estimator by using the orthogonality principle.

We want to be able to approximate a vector x by

$x=\hat{x}+e\,$

where

$\hat{x}=\sum_i c_{i}p_{i}$

is the approximation of x as a linear combination of vectors in the subspace W spanned by $p_{1},p_{2},\ldots.$ Therefore, we want to be able to solve for the coefficients, c_i, so that we may write our approximation in known terms.

By the orthogonality theorem, the square norm of the error vector, $\left\Vert e\right\Vert ^{2}$, is minimized when, for all j,

$\left\langle x-\sum_i c_{i}p_{i},p_{j}\right\rangle =0.$

Developing this equation, we obtain

$\left\langle x,p_{j}\right\rangle =\left\langle \sum_i c_{i}p_{i},p_{j}\right\rangle =\sum_i c_{i}\left\langle p_{i},p_{j}\right\rangle.$

If there is a finite number n of vectors p_i, one can write this equation in matrix form as

$\begin{bmatrix} \left\langle x,p_{1}\right\rangle \\ \left\langle x,p_{2}\right\rangle \\ \vdots\\ \left\langle x,p_{n}\right\rangle \end{bmatrix} = \begin{bmatrix} \left\langle p_{1},p_{1}\right\rangle & \left\langle p_{2},p_{1}\right\rangle & \cdots & \left\langle p_{n},p_{1}\right\rangle \\ \left\langle p_{1},p_{2}\right\rangle & \left\langle p_{2},p_{2}\right\rangle & \cdots & \left\langle p_{n},p_{2}\right\rangle \\ \vdots & \vdots & \ddots & \vdots\\ \left\langle p_{1},p_{n}\right\rangle & \left\langle p_{2},p_{n}\right\rangle & \cdots & \left\langle p_{n},p_{n}\right\rangle \end{bmatrix} \begin{bmatrix} c_{1}\\ c_{2}\\ \vdots\\ c_{n}\end{bmatrix}.$

Assuming the p_i are linearly independent, the Gramian matrix can be inverted to obtain

$\begin{bmatrix} c_{1}\\ c_{2}\\ \vdots\\ c_{n}\end{bmatrix} = \begin{bmatrix} \left\langle p_{1},p_{1}\right\rangle & \left\langle p_{2},p_{1}\right\rangle & \cdots & \left\langle p_{n},p_{1}\right\rangle \\ \left\langle p_{1},p_{2}\right\rangle & \left\langle p_{2},p_{2}\right\rangle & \cdots & \left\langle p_{n},p_{2}\right\rangle \\ \vdots & \vdots & \ddots & \vdots\\ \left\langle p_{1},p_{n}\right\rangle & \left\langle p_{2},p_{n}\right\rangle & \cdots & \left\langle p_{n},p_{n}\right\rangle \end{bmatrix}^{-1} \begin{bmatrix} \left\langle x,p_{1}\right\rangle \\ \left\langle x,p_{2}\right\rangle \\ \vdots\\ \left\langle x,p_{n}\right\rangle \end{bmatrix},$

thus providing an expression for the coefficients c_i of the minimum mean square error estimator.

Notes

1. ^ Kay, p.386
2. ^ See the article minimum mean square error.

References

• Kay, S. M. (1993). Fundamentals of Statistical Signal Processing: Estimation Theory. Prentice Hall. ISBN 0-13-042268-1. 
• Moon, Todd K. (2000). Mathematical Methods and Algorithms for Signal Processing. Prentice-Hall. ISBN 0-201-36186-8