Membership function (mathematics)

The membership function of a fuzzy set is a generalization of the indicator function in classical sets. In fuzzy logic, it represents the degree of truth as an extension of valuation. Degrees of truth are often confused with probabilities, although they are conceptually distinct, because fuzzy truth represents membership in vaguely defined sets, not likelihood of some event or condition. Membership functions were introduced by Zadeh in the first paper on fuzzy sets (1965).

Definition

For any set X, a membership function on X is any function from X to the real unit interval [0,1].

Membership functions on X represent fuzzy subsets of X. The membership function which represents a fuzzy set $\tilde A$ is usually denoted by μ_A. For an element x of X, the value μ_A(x) is called the membership degree of x in the fuzzy set $\tilde A.$ The membership degree μ_A(x) quantifies the grade of membership of the element x to the fuzzy set $\tilde A.$ The value 0 means that x is not a member of the fuzzy set; the value 1 means that x is fully a member of the fuzzy set. The values between 0 and 1 characterize fuzzy members, which belong to the fuzzy set only partially.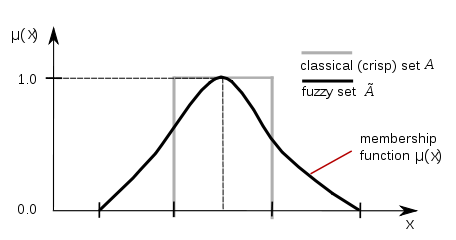

Membership function of a fuzzy set

Sometimes,^[1] a more general definition is used, where membership functions take values in an arbitrary fixed algebra or structure L; usually it is required that L be at least a poset or lattice. The usual membership functions with values in [0, 1] are then called [0, 1]-valued membership functions.

Capacity

One application of membership functions is as capacities in decision theory.

In decision theory, a capacity is defined as a function, ν from S, the set of subsets of some set, into [0,1], such that ν is set-wise monotone and is normalized (i.e. $\nu(\empty) = 0, \nu(\Omega)=1).$ Clearly this is a generalization of a probability measure, where the probability axiom of countability is weakened. A capacity is used as a subjective measure of the likelihood of an event, and the "expected value" of an outcome given a certain capacity can be found by taking the Choquet integral over the capacity.

See also

• Defuzzification
• Fuzzy measure theory
• fuzzy set operations
• Rough set

References

1. ^ First in Goguen (1967).

Bibliography

• Zadeh L.A., 1965, "Fuzzy sets". Information and Control 8: 338–353. [1]

• Goguen J.A, 1967, "L-fuzzy sets". Journal of Mathematical Analysis and Applications 18: 145–174

External links

• Fuzzy Image Processing