Clustering coefficient

In graph theory, a clustering coefficient is a measure of degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties (Holland and Leinhardt, 1971;^[1] Watts and Strogatz, 1998^[2]). In real-world networks, this likelihood tends to be greater than the average probability of a tie randomly established between two nodes (Holland and Leinhardt, 1971; Watts and Strogatz, 1998).

Two versions of this measure exist: the global and the local. The global version was designed to give an overall indication of the clustering in the network, whereas the local gives an indication of the embeddedness of single nodes.

Global clustering coefficient

The global clustering coefficient is based on triplets of nodes. A triplet consists of three nodes that are connected by either two (open triplet) or three (closed triplet) undirected ties. A triangle consists of three closed triplets, one centred on each of the nodes. The global clustering coefficient is the number of closed triplets (or 3 x triangles) over the total number of triplets (both open and closed). The first attempt to measure it was made by Luce and Perry (1949).^[3] This measure gives an indication of the clustering in the whole network (global), and can be applied to both undirected and directed networks (often called transitivity, see Wasserman and Faust, 1994, page 243^[4]).

Formally, it has been defined as:

$C = \frac{3 \times \mbox{number of triangles}}{\mbox{number of connected triples of vertices}} = \frac{\mbox{number of closed triplets}}{\mbox{number of connected triples of vertices}}.$

A generalisation to weighted networks was proposed by Opsahl and Panzarasa (2009),^[5] and a redefinition to two-mode networks (both binary and weighted) by Opsahl (2009).^[6]

Local clustering coefficient

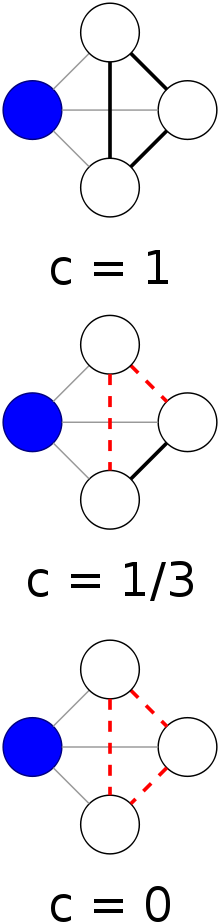Example local clustering coefficient on an undirected graph. The local clustering coefficient of the light blue node is computed as the proportion of connections among its neighbors which are actually realized compared with the number of all possible connections. In the figure, the light blue node has three neighbours, which can have a maximum of 3 connections among them. In the top part of the figure all three possible connections are realised (thick black segments), giving a local clustering coefficient of 1. In the middle part of the figure only one connection is realised (thick black line) and 2 connections are missing (dotted red lines), giving a local cluster coefficient of 1/3. Finally, none of the possible connections among the neighbours of the light blue node are realised, producing a local clustering coefficient value of 0.

The local clustering coefficient of a vertex in a graph quantifies how close its neighbors are to being a clique (complete graph). Duncan J. Watts and Steven Strogatz introduced the measure in 1998 to determine whether a graph is a small-world network.

A graph G = (V,E) formally consists of a set of vertices V and a set of edges E between them. An edge e_ij connects vertex i with vertex j.

The neighbourhood N for a vertex v_i is defined as its immediately connected neighbours as follows:

$N_i = \{v_j : e_{ij} \in E \and e_{ji} \in E\}.$

We define k_i as the number of vertices, | N_i | , in the neighbourhood, N_i, of a vertex.

The local clustering coefficient C_i for a vertex v_i is then given by the proportion of links between the vertices within its neighbourhood divided by the number of links that could possibly exist between them. For a directed graph, e_ij is distinct from e_ji, and therefore for each neighbourhood N_i there are k_i(k_i − 1) links that could exist among the vertices within the neighbourhood (k_i is the total (in + out) degree of the vertex). Thus, the local clustering coefficient for directed graphs is given as

$C_i = \frac{|\{e_{jk}\}|}{k_i(k_i-1)} : v_j,v_k \in N_i, e_{jk} \in E.$

An undirected graph has the property that e_ij and e_ji are considered identical. Therefore, if a vertex v_i has k_i neighbours, $\frac{k_i(k_i-1)}{2}$ edges could exist among the vertices within the neighbourhood. Thus, the local clustering coefficient for undirected graphs can be defined as

$C_i = \frac{2|\{e_{jk}\}|}{k_i(k_i-1)} : v_j,v_k \in N_i, e_{jk} \in E.$

Let λ_G(v) be the number of triangles on $v \in V(G)$ for undirected graph G. That is, λ_G(v) is the number of subgraphs of G with 3 edges and 3 vertices, one of which is v. Let τ_G(v) be the number of triples on $v \in G$. That is, τ_G(v) is the number of subgraphs (not necessarily induced) with 2 edges and 3 vertices, one of which is v and such that v is incident to both edges. Then we can also define the clustering coefficient as

$C_i = \frac{\lambda_G(v)}{\tau_G(v)}.$

It is simple to show that the two preceding definitions are the same, since

$\tau_G(v) = C({k_i},2) = \frac{1}{2}k_i(k_i-1).$

These measures are 1 if every neighbour connected to v_i is also connected to every other vertex within the neighbourhood, and 0 if no vertex that is connected to v_i connects to any other vertex that is connected to v_i.

Network average clustering coefficient

The clustering coefficient for the whole network is given by Watts and Strogatz^[2] as the average of the local clustering coefficients of all the vertices n :

$\bar{C} = \frac{1}{n}\sum_{i=1}^{n} C_i.$

A graph is considered small-world, if its average clustering coefficient $\bar{C}$ is significantly higher than a random graph constructed on the same vertex set, and if the graph has approximately the same mean-shortest path length as its corresponding random graph.

A generalisation to weighted networks was proposed by Barrat et al. (2004),^[7] and a redefinition to bipartite graphs (also called two-mode networks) by Latapy et al. (2008)^[8] and Opsahl (2009).^[6]

This formula is not, by default, defined for graphs with isolated vertices; see Kaiser, (2008)^[9] and Barmpoutis et al.^[10] The networks with the largest possible average clustering coefficient are found to have a modular structure, and at the same time, they have the smallest possible average distance among the different nodes.^[10]

References

1. ^ P. W. Holland and S. Leinhardt (1971). "Transitivity in structural models of small groups". Comparative Group Studies 2: 107–124. 
2. ^ ^{a b} D. J. Watts and Steven Strogatz (June 1998). "Collective dynamics of 'small-world' networks". Nature 393 (6684): 440–442. Bibcode 1998Natur.393..440W. doi:10.1038/30918. PMID 9623998. http://tam.cornell.edu/tam/cms/manage/upload/SS_nature_smallworld.pdf. 
3. ^ R. D. Luce and A. D. Perry (1949). "A method of matrix analysis of group structure". Psychometrika 14 (1): 95–116. doi:10.1007/BF02289146. PMID 18152948. 
4. ^ Stanley Wasserman, Kathrine Faust, 1994. Social Network Analysis: Methods and Applications. Cambridge: Cambridge University Press.
5. ^ Tore Opsahl and Pietro Panzarasa (2009). "Clustering in Weighted Networks". Social Networks 31 (2): 155–163. doi:10.1016/j.socnet.2009.02.002. http://toreopsahl.com/2009/04/03/article-clustering-in-weighted-networks/. 
6. ^ ^{a b} Tore Opsahl (2009). "Clustering in Two-mode Networks". Conference and Workshop on Two-Mode Social Analysis (Sept 30-Oct 2, 2009). http://toreopsahl.com/2009/09/11/clustering-in-two-mode-networks/. 
7. ^ A. Barrat and M. Barthelemy and R. Pastor-Satorras and A. Vespignani (2004). "The architecture of complex weighted networks". Proceedings of the National Academy of Sciences 101 (11): 3747–3752. arXiv:cond-mat/0311416. Bibcode 2004PNAS..101.3747B. doi:10.1073/pnas.0400087101. PMC 374315. PMID 15007165. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=374315. 
8. ^ M. Latapy and C. Magnien and N. Del Vecchio (2008). "Basic Notions for the Analysis of Large Two-mode Networks". Social Networks 30 (1): 31–48. doi:10.1016/j.socnet.2007.04.006. 
9. ^ Marcus kaiser (2008). "Mean clustering coefficients: the role of isolated nodes and leafs on clustering measures for small-world networks". New Journal of Physics 10 (8): 083042. Bibcode 2008NJPh...10h3042K. doi:10.1088/1367-2630/10/8/083042. http://stacks.iop.org/1367-2630/10/i=8/a=083042. 
10. ^ ^{a b} D. Barmpoutis and R. M. Murray (2010). "Networks with the Smallest Average Distance and the Largest Average Clustering". arXiv:1007.4031 [q-bio.MN].