- Degree matrix
-
In the mathematical field of graph theory the degree matrix is a diagonal matrix which contains information about the degree of each vertex. It is used together with the adjacency matrix to construct the Laplacian matrix of a graph.
Definition
Given a graph G = (V,E) with
 the degree matrix D for G is a
the degree matrix D for G is a  square matrix defined as
square matrix defined asExample
Vertex labeled graph Degree matrix 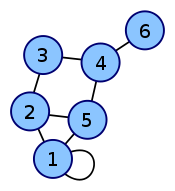

For an undirected graph, the degree of a vertex is the number of edges incident to the vertex. This means that each loop is counted twice. This is because each edge has two endpoints and each endpoint adds to the degree.
- The degree matrix of a k-regular graph has a constant diagonal of k
Categories:- Algebraic graph theory
- Matrices
Wikimedia Foundation. 2010.

