- Complement graph
-
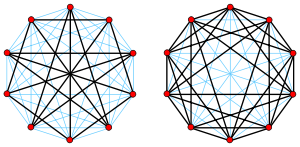 The Petersen graph (on the left) and its complement graph (on the right).
The Petersen graph (on the left) and its complement graph (on the right).
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and removes all the edges that were previously there. It is not, however, the set complement of the graph; only the edges are complemented.
Formal construction
Let G = (V, E) be a simple graph and let K consist of all 2-element subsets of V. Then H = (V, K \ E) is the complement of G.
Applications and examples
Several graph-theoretic concepts are related to each other via complement graphs:
- The complement of an edgeless graph is a complete graph and vice versa.
- An independent set in a graph is a clique in the complement graph and vice versa.
- The complement of any triangle-free graph is a claw-free graph.
- A self-complementary graph is a graph that is isomorphic to its own complement.
- Cographs are defined as the graphs that can be built up from disjoint union and complementation operations, and form a self-complementary family of graphs: the complement of any cograph is another (possibly different) cograph.
References
- Bondy, John Adrian; Murty, U. S. R. (1976), Graph Theory with Applications, North-Holland, ISBN 0-444-19451-7, http://www.ecp6.jussieu.fr/pageperso/bondy/books/gtwa/gtwa.html, pages 6 and 29.
- Diestel, Reinhard (2005), Graph Theory (3rd ed.), Springer, ISBN 3-540-26182-6. Electronic edition, page 4.
Categories:
Wikimedia Foundation. 2010.
