Morley's trisector theorem

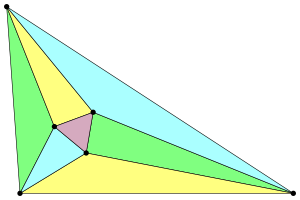
In plane geometry, Morley's trisector theorem states that in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle, called the Morley triangle. The theorem was discovered in 1899 by Anglo-American mathematician Frank Morley. It has various generalizations; in particular, if all of the trisectors are intersected, one obtains four other equilateral triangles. Morley's Theorem is one of the most surprising and beautiful theorems in plane geometry.

Proofs

There are many proofs of Morley's theorem, some of which are very technical.^[1] Several early proofs were based on delicate trigonometric calculations. The first published geometric proof was given by M.T.Naraniengar in 1909.^[2] Recent proofs include an algebraic proof by Alain Connes (1988, 2004) extending the theorem to general fields, and John Conway's elementary geometry proof.^[3][4] The latter starts with an equilateral triangle and shows that a triangle may be built around it which will be similar to any selected triangle. Interestingly, Morley's theorem does not hold in spherical^[5] and hyperbolic geometry.

Fig 1.   Elementary proof of Morley's trisector theorem

Arguably the best proof uses the trigonometric identity :

sin 3θ ≡ 4 sin θ sin(60°+θ) sin(120°+θ).

Points D,E,F are constructed on BC as shown. Clearly α+β+γ = 60° therefore ∠CYA = 120°+β and the angles of ΔXEF are α, 60°+β, 60°+γ. Now sin(60°+β) = DX/XE and AC/sin(120°+β) = AY/sin γ by the sine rule, so the height h of ΔABC is given by

h = AB sin 3β = 4AB.AC.DX sin β sin γ / (XE.AY)

  = AC sin 3γ = 4AC.AB.DX sin γ sin β / (XF.AZ).

As the numerators are equal, XE.AY = XF.AZ. But ∠EXF = ∠ZAY and the sides about these angles are in the same ratio (because XE/XF = AZ/AY) so the triangles XEF and AZY must be similar. Thus the base angles of ΔAZY are 60°+β and 60°+γ. Similar arguments yield the base angles of ΔBXZ and ΔCYX and all the angles in the figure can now be easily determined.

The result can also be proved by the technique of reverse reconstruction.

Morley's triangles

Morley's theorem entails 18 equilateral triangles. The triangle described in the trisector theorem above, called the first Morley triangle, has vertices given in trilinear coordinates relative to a triangle ABC as follows:

A-vertex = 1 : 2 cos(C/3) : 2 cos(B/3)

B-vertex = 2 cos(C/3) : 1 : 2 cos(A/3)

C-vertex = 2 cos(B/3) : 2 cos(A/3) : 1

Another of Morley's equilateral triangle that is also central triangle is called the second Morley triangle and is given by these vertices:

A-vertex = 1 : 2 cos(C/3 − 2π/3) : 2 cos(B/3 − 2π/3)

B-vertex = 2 cos(C/3 − 2π/3) : 1 : 2 cos(A/3 − 2π/3)

C-vertex = 2 cos(B/3 − 2π/3) : 2 cos(A/3 − 2π/3) : 1

The third of Morley's 18 equilateral triangles that is also central triangle is called the third Morley triangle and is given by these vertices:

A-vertex = 1 : 2 cos(C/3 − 4π/3) : 2 cos(B/3 − 4π/3)

B-vertex = 2 cos(C/3 − 4π/3) : 1 : 2 cos(A/3 − 4π/3)

C-vertex = 2 cos(B/3 − 4π/3) : 2 cos(A/3 − 4π/3) : 1

The first, second, and third Morley triangles are pairwise homothetic. Another homothetic triangle is formed by the three points X on the circumcircle of triangle ABC at which the line XX ⁻¹ is tangent to the circumcircle, where X ⁻¹ denotes the isogonal conjugate of X. This equilateral triangle, called the circumtangential triangle, has these vertices:

A-vertex = csc(C/3 − B/3) : csc(B/3 + 2C/3) : −csc(C/3 + 2B/3)

B-vertex = −csc(A/3 + 2C/3) : csc(A/3 − C/3) : csc(C/3 + 2A/3)

C-vertex = csc(A/3 + 2B/3) : −csc(B/3 + 2A/3) : csc(B/3 − A/3)

A fifth equilateral triangle, also homothetic to others, is obtained by rotating the circumtangential triangle π/6 about its center. Called the circumnormal triangle, its vertices are as follows:

A-vertex = sec(C/3 − B/3) : −sec(B/3 + 2C/3) : −sec(C/3 + 2B/3)

B-vertex = −sec(A/3 + 2C/3) : sec(A/3 − C/3) : −sec(C/3 + 2A/3)

C-vertex = −sec(A/3 + 2B/3) : −sec(B/3 + 2A/3) : sec(B/3 − A/3)

An operation called "extraversion" can be used to obtain one of the 18 Morley triangles from another. Each triangle can be extraverted in three different ways; the 18 Morley triangles and 27 extravert pairs of triangles form the 18 vertices and 27 edges of the Pappus graph.^[6]

Related triangle centers

The centroid of the first Morley triangle is given by

Morley center = X(356) = cos(A/3) + 2 cos(B/3)cos(C/3) : cos(B/3) + 2 cos(C/3)cos(A/3) : cos(C/3) + 2 cos(A/3)cos(B/3)

The first Morley triangle is perspective to triangle ABC, and the perspector is the point

1st Morley-Taylor-Marr center = X(357) = sec(A/3) : sec(B/3) : sec(C/3)

Notes

1. ^ Bogomolny, Alexander, Morley's Miracle, Cut-the-knot, http://www.cut-the-knot.org/triangle/Morley/index.shtml, retrieved 2010-01-02 
2. ^ Coxeter (1967).
3. ^ J. Conway's proof, from Bogomolny.
4. ^ Conway, John (2006), "The Power of Mathematics", in Blackwell, Alan; Mackay, David, Power, Cambridge University Press, pp. 36–50, ISBN 978-0-521-82377-7, http://www.cs.toronto.edu/~mackay/conway.pdf, retrieved 2010-10-08 
5. ^ Morley's Theorem in Spherical Geometry, Java applet.
6. ^ Guy (2007).

References

• Connes, Alain (1998), "A new proof of Morley's theorem", Publications Mathématiques de l'IHÉS S88: 43–46, http://www.numdam.org/item?id=PMIHES_1998__S88__43_0 .
• Connes, Alain (December 2004), "Symmetries", European Mathematical Society Newsletter 54, http://www.ems-ph.org/journals/newsletter/pdf/2004-12-54.pdf .
• Coxeter, H. S. M.; Greitzer, S. L. (1967), "Geometry Revisited", The Mathematical Association of America, LCCN 67--20607 
• Francis, Richard L. (2002), "Modern Mathematical Milestones: Morley's Mystery", Missouri Journal of Mathematical Sciences 14 (1), http://www.math-cs.ucmo.edu/~mjms/2002.1/francis9.pdf .
• Guy, Richard K. (2007), "The lighthouse theorem, Morley & Malfatti—a budget of paradoxes", American Mathematical Monthly 114 (2): 97–141, JSTOR 27642143, MR2290364, http://www.math.ucalgary.ca/files/publications/3414848.pdf .
• Oakley, C. O.; Baker, J. C. (1978), "The Morley trisector theorem", American Mathematical Monthly 85 (9): 737–745, doi:10.2307/2321680, JSTOR 2321680 .
• Taylor, F. Glanville; Marr, W. L. (1913–14), "The six trisectors of each of the angles of a triangle", Proceedings of the Edinburgh Mathematical Society 33: 119–131 .

External links

• Morleys Theorem at MathWorld
• Morley's Trisection Theorem at MathPages
• Morley's Theorem by Oleksandr Pavlyk, The Wolfram Demonstrations Project.