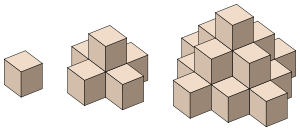
Octahedral number

146 magnetic balls, packed in the form of an octahedron

In number theory, an octahedral number is a figurate number that represents the number of spheres in an octahedron formed from close-packed spheres. The nth octahedral number O_n can be obtained by the formula:^[1]

$O_n={n(2n^2 + 1) \over 3}.$

The first few octahedral numbers are:

1, 6, 19, 44, 85, 146, 231, 344, 489, 670, 891 (sequence A005900 in OEIS).

Properties and applications

The octahedral numbers have a generating function

$\frac{z(z+1)^2}{(z-1)^4} = \sum_{n=1}^{\infty} O_n z^n = z +6z^2 + 19z^3 + \cdots .$

Sir Frederick Pollock conjectured in 1850 that every number is the sum of at most 7 octahedral numbers: see Pollock octahedral numbers conjecture.^[2]

In chemistry, octahedral numbers may be used to describe the numbers of atoms in octahedral clusters; in this context they are called magic numbers.^[3][4]

Relation to other figurate numbers

Square pyramids

Square pyramids in which each layer has a centered square number of cubes. The total number of cubes in each pyramid is an octahedral number.

An octahedral packing of spheres may be partitioned into two square pyramids, one upside-down underneath the other, by splitting it along a square cross-section. Therefore, the nth octahedral number O_n can be obtained by adding two consecutive square pyramidal numbers together:^[1]

O_n = P_{n − 1} + P_n.

Tetrahedra

If O_n is the nth octahedral number and T_n is the nth tetrahedral number then

O_n + 4T_{n − 1} = T_{2n − 1}.

This represents the geometric fact that gluing a tetrahedron onto each of four non-adjacent faces of an octahedron produces a tetrahedron of twice the size. Another relation between octahedral numbers and tetrahedral numbers is also possible, based on the fact that an octahedron may be divided into four tetrahedra each having two adjacent original faces (or alternatively, based on the fact that each square pyramidal number is the sum of two tetrahedral numbers):

O_n = T_n + 2T_{n − 1} + T_{n − 2}.

Cubes

If two tetrahedra are attached to opposite faces of an octahedron, the result is a rhombohedron.^[5] The number of close-packed spheres in the rhombohedron is a cube, justifying the equation

O_n + 2T_{n − 1} = n³.

Centered squares

The difference between two consecutive octahedral numbers is a centered square number:^[1]

O_n − O_{n − 1} = C_4,n = n² + (n − 1)².

Therefore, an octahedral number also represents the number of points in a square pyramid formed by stacking centered squares; for this reason, in his book Arithmeticorum libri duo (1575), Francesco Maurolico called these numbers "pyramides quadratae secundae".^[6]

The number of cubes in an octahedron formed by stacking centered squares is a centered octahedral number, the sum of two consecutive octahedral numbers. These numbers are

1, 7, 25, 63, 129, 231, 377, 575, 833, 1159, 1561, 2047, 2625, ... (sequence A001845 in OEIS)

given by the formula

$O_n+O_{n-1}=\frac{(2n+1)(2n^2+2n+3)}{3}.$

References

1. ^ ^{a b c} Conway, John Horton; Guy, Richard K. (1996), The Book of Numbers, Springer-Verlag, p. 50, ISBN 9780387979939 .
2. ^ Dickson, L. E. (2005), History of the Theory of Numbers, Vol. 2: Diophantine Analysis, New York: Dover, pp. 22–23, http://books.google.com/books?id=eNjKEBLt_tQC&pg=PA22 .
3. ^ Teo, Boon K.; Sloane, N. J. A. (1985), "Magic numbers in polygonal and polyhedral clusters", Inorganic Chemistry 24 (26): 4545–4558, doi:10.1021/ic00220a025, http://www2.research.att.com/~njas/doc/magic1/magic1.pdf .
4. ^ Feldheim, Daniel L.; Foss, Colby A. (2002), Metal nanoparticles: synthesis, characterization, and applications, CRC Press, p. 76, ISBN 9780824706043, http://books.google.com/books?id=-u9tVYWfRcMC&pg=PA76 .
5. ^ Burke, John G. (1966), Origins of the science of crystals, University of California Press, p. 88, http://books.google.com/books?id=qvxPbZtJu8QC&pg=PA88 .
6. ^ Tables of integer sequences from Arithmeticorum libri duo, retrieved 2011-04-07.

External links

• Weisstein, Eric W., "Octahedral Number" from MathWorld.