Witch of Agnesi

In mathematics, the witch of Agnesi (Italian pronunciation: [a.ˈɲe.zi]), sometimes called the witch of Maria Agnesi is the curve defined as follows.

The Witch of Agnesi with labeled points

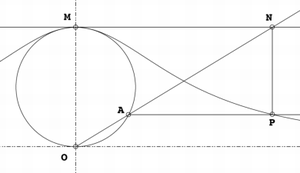
Starting with a fixed circle, a point O on the circle is chosen. For any other point A on the circle, the secant line OA is drawn. The point M is diametrically opposite O. The line OA intersects the tangent of M at the point N. The line parallel to OM through N, and the line perpendicular to OM through A intersect at P. As the point A is varied, the path of P is the witch.

The curve is asymptotic to the line tangent to the fixed circle through the point O.

Equations

An animation showing the construction of the Witch of Agnesi

Suppose the point O is the origin, and that M is on the positive y-axis. Suppose the radius of the circle is a.

Then the curve has Cartesian equation

$\!y = \frac{8a^3}{x^2+4a^2}$.

Note that if a=1/2, then this equation becomes rather simple:

$\!y = \frac{1}{x^2+1}.$

Parametrically, if $\theta\,$ is the angle between OM and OA, measured clockwise, then the curve is defined by the equations

$\!x = 2a \tan \theta,\ y = 2a \cos ^2 \theta.\,$

Another parameterization, with $\theta\,$ being the angle between OA and the x-axis, increasing anti-clockwise is

$\!x = 2a \cot \theta,\ y=2a\sin ^2 \theta.\,$

Properties

The Witch of Agnesi with parameters a=1, a=2, a=4, and a=8

• The area between the Witch and its asymptote is four times the area of the fixed circle (i.e., 4πa²).

• The volume of revolution of the Witch, about its asymptote, is 4π²a³.

• The centroid of the curve is at

$\!\left(0,a\right)$,

which is the same as that of the generating circle (diameter = 2a).

History

The curve was studied by Pierre de Fermat in 1630. In 1703, Guido Grandi gave a construction for the curve. In 1718 Grandi suggested the name 'versoria' for the curve, the Latin term for sheet, the rope which turns (adjusts the trim of) the sail, and used the Italian word for it, 'versiera', a hint to sinus versus that appeared in his construction.^[1]

In 1748, Maria Agnesi published her famous summation treatise Instituzioni analitiche ad uso della gioventù italiana, in which the curve was named according to Grandi, 'versiera'. ^[1] Coincidentally, the contemporary Italian word 'Aversiera'/'Versiera', derived from Latin 'Adversarius', a nickname for Devil, "Adversary of God", was synonymous with "witch".^[2] Probably for this reason Cambridge professor John Colson mistranslated the name of the curve thusly. Different modern works about Agnesi and about the curve suggest slightly different guesses how exactly this mistranslation happened. ^[3][4][5] Struik mentions that:

The word [versiera] is derived from Latin vertere, to turn, but is also an abbreviation of Italian avversiera, female devil. Some wit in England once translated it 'witch', and the silly pun is still lovingly preserved in most of our textbooks in English language. ... The curve had already appeared in the writings of Fermat (Oeuvres, I, 279-280; III, 233-234) and of others; the name versiera is from Guido Grandi (Quadratura circuli et hyperbolae, Pisa, 1703). The curve is type 63 in Newton's classification. ... The first to use the term 'witch' in this sense may have been B. Williamson, Integral calculus, 7 (1875), 173;^[6] see Oxford English Dictionary.

On the other hand, Stephen Stigler suggests that Grandi himself "may have been indulging in a play on words".^[7]

The Witch of Agnesi is also a fiction novel by Robert Spiller, in which a teacher gives a version of the history of the term.^[8]

See also

• Cauchy distribution
• Lorentzian function

References

1. ^ ^{a b} C. Truesdell, "Correction and Additions for 'Maria Gaetana Agnesi'", Archive for History of Exact Science 43 (1991), 385-386. doi:10.1007/BF00374764
   • Per Grandi: "...nata da' seni versi, che da me suole chiamarsi la Versiera in latino pero Versoria..."
2. ^ "Vocabolario dell'uso toscano", 1 By Pietro Fanfani, p. 334
3. ^ Women in Mathematics By Lynn M. Osen (1975) p. 45
4. ^ "Fermat's Enigma" by Simon Singh p. 100
5. ^ The universal book of mathematics: from Abracadabra to Zeno's paradoxes By David J. Darling (2004) p. 8
6. ^ "173 Find the area between the witch of Agnesi xy² = 4a²(2a − x) and its asymptote." (Oxford English Dictionary)
7. ^ S.M.Stigler, "Cauchy and the witch of Agnesi: An historical note on the Cauchy distribution", Biometrika, 1974, vol. 61, no.2 p. 375-380
8. ^ Spiller, Robert (2006). The Witch of Agnesi. Palm Beach, FL: Medallion Press. ISBN 9781932815726. OCLC 71259167. 

Sources

• Weisstein, Eric W., "Witch of Agnesi" from MathWorld.
• "Witch of Agnesi" at MacTutor's Famous Curves Index
• "Cubique d'Agnesi" at Encyclopédie des Formes Mathématiques Remarquables (in French)
• "MacTutor biography of Agnesi". http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Agnesi.html. 
• "The Witch of Agnesi". John H. Lienhard. The Engines of Our Ingenuity. NPR. KUHF-FM Houston. 2002. No. 1741. Transcript.

External links

• Witch of Agnesi by Chris Boucher based on work by Eric W. Weisstein, The Wolfram Demonstrations Project.
• The Witch of Agnesi - Mathforum.org Java applet