Lebesgue covering dimension

Lebesgue covering dimension or topological dimension is one of several inequivalent notions of assigning a topological invariant dimension to a given topological space.

Definition

The covering dimension of a topological space X is defined to be the minimum value of n, such that every finite open cover $\mathcal{A}$ of X admits a finite open cover $\mathcal{B}$ of X which refines $\mathcal{A}$ in which no point is included in more than n+1 elements. If no such minimal n exists, the space is said to be of infinite covering dimension.

Examples

The n-dimensional Euclidean space $\mathbb{E}^n$ has covering dimension n.

A topological space is zero-dimensional with respect to the covering dimension if every open cover of the space has a refinement consisting of disjoint open sets so that any point in the space is contained in exactly one open set of this refinement.

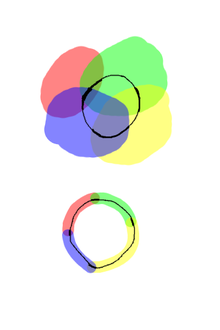
Any given open cover of the unit circle will have a refinement consisting of a collection of open arcs. The circle has dimension one, by this definition, because any such cover can be further refined to the stage where a given point x of the circle is contained in at most two open arcs. That is, whatever collection of arcs we begin with, some can be discarded or shrunk, such that the remainder still covers the circle, but with simple overlaps.

Similarly, any open cover of the unit disk in the two-dimensional plane can be refined so that any point of the disk is contained in no more than three open sets, while two are in general not sufficient. The covering dimension of the disk is thus two.

A non-technical illustration of these examples below.

Below is a refinement of a cover (above) of a circular line (black). Notice how in the refinement no point on the line is contained in more than two sets. Note also how the sets link to each other to form a "chain".

Below left is a refinement of a cover (above) of a planar shape (dark) so that all points in the shape are contained in at most three sets. Below right is an attempt to refine the cover so that no point would be contained in more than two sets. This fails in the intersection of set borders. Thus, a planar shape isn't "webby" or cannot be covered with "chains", but is in a sense thicker; i.e., its topological dimension must be higher than one.

Properties

• Homeomorphic spaces have the same covering dimension.

• The Lebesgue covering dimension coincides with the affine dimension of a finite simplicial complex; this is the Lebesgue covering theorem.

• The covering dimension of a normal space is less than or equal to the large inductive dimension.

• Covering dimension of a normal space X is $\le n$ if and only if for any closed subset A of X, if $f:A\rightarrow S^n$ is continuous, then there is an extension of f to $g:X\rightarrow S^n$. Here, Sⁿ is the n dimensional sphere.

• (Ostrand's theorem on colored dimension.) A normal space X satisfies the inequality $\dim X\le m \ge0$ if and only if for every locally finite open cover $\mathcal U= \{U_\alpha\}_{\alpha\in\mathcal A}$ of the space X there exists an open cover $\mathcal V$ of the space X which can be represented as the union of n + 1 families $\mathcal V_1, \mathcal V_2,\dots,\mathcal V_{n+1}$, where $\mathcal V_i=\{V_{i,\alpha}\}_{\alpha\in\mathcal A}$, such that sets in each $\mathcal V_i$ do not interect and $V_{i,\alpha}\subset U_\alpha$ for each i and α.

History

The first formal definition of covering dimension was given by Eduard Čech, it was based on earlier result of Henri Lebesgue.

See also

• Dimension theory
• Metacompact space
• Point-finite collection

References

Historical references

• Karl Menger, General Spaces and Cartesian Spaces, (1926) Communications to the Amsterdam Academy of Sciences. English translation reprinted in Classics on Fractals, Gerald A.Edgar, editor, Addison-Wesley (1993) ISBN 0-201-58701-7
• Karl Menger, Dimensionstheorie, (1928) B.G Teubner Publishers, Leipzig.
• A. R. Pears, Dimension Theory of General Spaces, (1975) Cambridge University Press. ISBN 0-521-20515-8

Modern references

• V.V. Fedorchuk, The Fundamentals of Dimension Theory, appearing in Encyclopaedia of Mathematical Sciences, Volume 17, General Topology I, (1993) A. V. Arkhangel'skii and L. S. Pontryagin (Eds.), Springer-Verlag, Berlin ISBN 3-540-18178-4.